题目内容
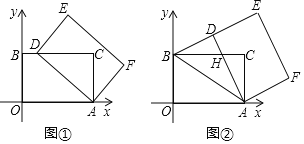
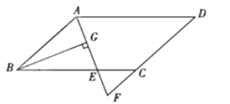
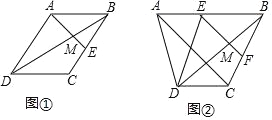
【题目】探究:如图①,在ABCD中,E为BC的中点,AE与BD相交于点M.求证:![]() .
.
应用:如图②,在四边形ABCD中,AB∥CD,AB=2CD,点E、F分别为AB、BC的中点,EF与BD相交于点M,连结AC.若ME=3,则AC的长为 .
【答案】证明见解析 AC=9
【解析】
(1)根据四边形ABCD是平行四边形,从而得到线段间的位置关系,利用三角形相似即可解答.
(2)根据点E、F分别为AB、BC的中点,求出四边形BCDE为平行四边形,再利用中位线即可解答.
探究:证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠EBM=∠ADM,∠BEM=∠DAM,
∴△EBM∽△ADM,
∴![]() =
=![]() .
.
∵点E为BC的中点,
∴EB=![]() BC=
BC=![]() AD,
AD,
∴![]() =
=![]() ,
,
∴![]() =
=![]() .
.
应用:解:∵AB∥CD,AB=2CD,点E为AB的中点,
∴BE=![]() AB=CD,
AB=CD,
∴四边形BCDE为平行四边形.
又∵点F为BC的中点,
∴![]() =
=![]() .
.
∵ME=3,
∴EF=ME+MF=3+![]() =
=![]() .
.
∵点E、F分别为AB、BC的中点,
∴EF为△BAC的中位线,
∴AC=2EF=9.
故答案为:9.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
【题目】某通信公司策划了![]() 两种上网的月收费方式:
两种上网的月收费方式:
收费方式 | 月使用费/元 | 包时上网时间/ | 超时费/(元/ |
| 30 | 25 | 0.05 |
|
|
|
|
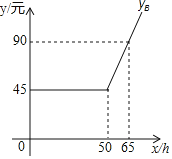
设每月上网时间为![]() ,方式
,方式![]() 的收费金额分别为
的收费金额分别为![]() (元),
(元),![]() (元),如图是
(元),如图是![]() 与
与![]() 之间函数关系的图象.(友情提示:若累计上网时间不超出包时上网时间,则只收月使用费;若累计上网时间超出包时上网时间,则对超出部分再加收超时费)
之间函数关系的图象.(友情提示:若累计上网时间不超出包时上网时间,则只收月使用费;若累计上网时间超出包时上网时间,则对超出部分再加收超时费)
(1)![]() ,
,![]() ,
,![]() ;
;
(2)求![]() 之间的函数解析式;
之间的函数解析式;
(3)若每月上网时间为31小时,请直接写出选择哪种方式能节省上网费.