题目内容
如图,直角三角形ABC位于第一象限,AB=3,AC=2,直角顶点A在直线 上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于
上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于 轴、
轴、 轴,若双曲线
轴,若双曲线 (
( )与△ABC有交点,则
)与△ABC有交点,则 的取值范围是(???? )
的取值范围是(???? )

A. ?? B.
?? B. ?? C.
?? C. ??? D.
??? D.
【答案】
B.
【解析】
试题分析:设直线y=x与BC交于E点,分别过A、E两点作x轴的垂线,垂足为D、F,则A(1,1),而AB=3,AC=2,则B(4,1),C(1,3),当反比例函数和直线BC相交时,求出b2-4ac的值,由此可求k的取值范围.
∵A点的坐标为(1,1),AB=3,AC=2,
B的坐标是(4,1),C的坐标是(1,3),
当反比例函数y= 过A点时,K值最小,代入得:k=1,
过A点时,K值最小,代入得:k=1,
即:k的最小值是1;
设直线BC的解析式是y=kx+b,
把B(4,1),C(1,3)代入得: ,
,
解得:  ,
,
∴直线BC的解析式是 ,
,
当反比例函数 与直线BC相交时,
与直线BC相交时,
 ,
,
即:2x2-11x+3k=0,
这里a=2,b=-11,c=3k,
b2-4ac=(-11)2-4×2×3k≥0,
解得:k≤ ,
,
k的取值范围为1 ≤k≤ .
.
故选B.
考点: 反比例函数综合题.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
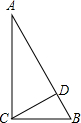 如图,直角三角形ABC中∠ACB=90°,CD是高,∠A=30°,AB=4.则BD=
如图,直角三角形ABC中∠ACB=90°,CD是高,∠A=30°,AB=4.则BD= 如图,直角三角形ABC的直角边AB=6,以AB为直径画半圆,若阴影部分的面积S1-S2=
如图,直角三角形ABC的直角边AB=6,以AB为直径画半圆,若阴影部分的面积S1-S2= 如图在直角三角形ABC的斜边AB上另作直角三角形ABD,并以AB为斜边,若BC=1,AC=m,AD=2,则BD等于( )
如图在直角三角形ABC的斜边AB上另作直角三角形ABD,并以AB为斜边,若BC=1,AC=m,AD=2,则BD等于( ) 如图,直角三角形ACB中,CD是斜边AB上的中线,若AC=8cm,BC=6cm,那么△ACD与△BCD的周长差为
如图,直角三角形ACB中,CD是斜边AB上的中线,若AC=8cm,BC=6cm,那么△ACD与△BCD的周长差为 如图,直角三角形ABC中,∠C=90°,P,E分别是边AB,BC上的点,D为△ABC外一点,DE⊥BC,DE=EC,BE=2EC,∠BDE=∠PEC,AD∥PE,AC=4,则线段BC的长为
如图,直角三角形ABC中,∠C=90°,P,E分别是边AB,BC上的点,D为△ABC外一点,DE⊥BC,DE=EC,BE=2EC,∠BDE=∠PEC,AD∥PE,AC=4,则线段BC的长为