题目内容
 (2013•河北一模)如图,过点P(-4,3)作x轴,y轴的垂线,分别交x轴、y轴于A,B两点,交双曲线y=
(2013•河北一模)如图,过点P(-4,3)作x轴,y轴的垂线,分别交x轴、y轴于A,B两点,交双曲线y=| k |
| x |
(1)点E的坐标是
(-4,-
)
| k |
| 4 |
(-4,-
)
,点F的坐标是| k |
| 4 |
(
,3)
| k |
| 3 |
(
,3)
;(均用含k的式子表示)| k |
| 3 |
(2)判断EF与AB的位置关系,并证明你的结论.
分析:(1)根据P点坐标可得到E点横坐标和F点纵坐标,代入函数解析式即可求出该两点的坐标;
(2)在Rt△PAB和Rt△PEF中,求出tan∠PAB和tan∠PEF,得到∠PAB=∠PEF,从而求出EF∥AB.
(2)在Rt△PAB和Rt△PEF中,求出tan∠PAB和tan∠PEF,得到∠PAB=∠PEF,从而求出EF∥AB.
解答:(1)解:∵点P(-4,3),
∴E点横坐标为-4,将x=-4代入y=
得,y=-
,故E(-4,-
);
∴F点纵坐标为3,将y=3代入y=
得,x=
,故F(
,3).
故答案为E(-4,-
);F(
,3).
(2)结论:EF∥AB.
证明:∵P(-4,3),
∴E(-4,-
),F(
,3),
即得:PE=3+
,PF=
+4,
在Rt△PAB中,tan∠PAB=
=
,
在Rt△PEF中,tan∠PEF=
=
=
,
∴tan∠PAB=tan∠PEF,
∴∠PAB=∠PEF,
∴EF∥AB.
∴E点横坐标为-4,将x=-4代入y=
| k |
| x |
| k |
| 4 |
| k |
| 4 |
∴F点纵坐标为3,将y=3代入y=
| k |
| x |
| k |
| 3 |
| k |
| 3 |
故答案为E(-4,-
| k |
| 4 |
| k |
| 3 |
(2)结论:EF∥AB.
证明:∵P(-4,3),
∴E(-4,-
| k |
| 4 |
| k |
| 3 |
即得:PE=3+
| k |
| 4 |
| k |
| 3 |
在Rt△PAB中,tan∠PAB=
| PB |
| PA |
| 4 |
| 3 |
在Rt△PEF中,tan∠PEF=
| PF |
| PE |
| ||
3+
|
| 4 |
| 3 |
∴tan∠PAB=tan∠PEF,
∴∠PAB=∠PEF,
∴EF∥AB.
点评:本题考查了反比例函数综合问题,熟悉函数图象上点的坐标特征和平行线的判定和性质是解题的关键.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
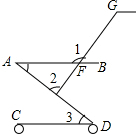 (2013•河北一模)如图是婴儿车的平面示意图,其中AB∥CD,∠1=120°,∠3=40°,那么∠2的度数为( )
(2013•河北一模)如图是婴儿车的平面示意图,其中AB∥CD,∠1=120°,∠3=40°,那么∠2的度数为( )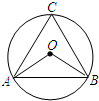 (2013•河北一模)如图,△ABC内接于⊙O,若∠OAB=28°,则∠C的大小为( )
(2013•河北一模)如图,△ABC内接于⊙O,若∠OAB=28°,则∠C的大小为( )