题目内容
【题目】如图,⊙O中,FG、AC是直径,AB是弦,FG⊥AB,垂足为点P,过点C的直线交AB的延长线于点D,交GF的延长线于点E,已知AB=4,⊙O的半径为 ![]() .
. 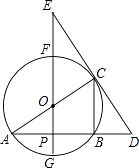
(1)分别求出线段AP、CB的长;
(2)如果OE=5,求证:DE是⊙O的切线;
(3)如果tan∠E= ![]() ,求DE的长.
,求DE的长.
【答案】
(1)解:∵AC为直径,
∴∠ABC=90°,
在Rt△ABC中,AC=2 ![]() ,AB=4,
,AB=4,
∴BC= ![]() =2,
=2,
∵直径FG⊥AB,
∴AP=BP= ![]() AB=2
AB=2
(2)证明∵AP=BP,AO=OC
∴OP为△ABC的中位线,
∴OP= ![]() BC=1,
BC=1,
∴ ![]() =
= ![]() ,
,
而 ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∵∠EOC=∠AOP,
∴△EOC∽△AOP,
∴∠OCE=∠OPA=90°,
∴OC⊥DE,
∴DE是⊙O的切线
(3)解:∵BC∥EP,
∴∠DCB=∠E,
∴tan∠DCB=tan∠E= ![]()
在Rt△BCD中,BC=2,tan∠DCB= ![]() =
= ![]() ,
,
∴BD=3,
∴CD= ![]() =
= ![]() ,
,
∵BC∥EP,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴DE= ![]()
【解析】(1)根据圆周角定理由AC为直径得∠ABC=90°,在Rt△ABC中,根据勾股定理可计算出BC=2,再根据垂径定理由直径FG⊥AB得到AP=BP= ![]() AB=2;(2)易得OP为△ABC的中位线,则OP=
AB=2;(2)易得OP为△ABC的中位线,则OP= ![]() BC=1,再计算出
BC=1,再计算出 ![]() =
= ![]() =
= ![]() ,根据相似三角形的判定方法得到△EOC∽△AOP,根据相似的性质得到∠OCE=∠OPA=90°,然后根据切线的判定定理得到DE是⊙O的切线;(3)根据平行线的性质由BC∥EP得到∠DCB=∠E,则tan∠DCB=tan∠E=
,根据相似三角形的判定方法得到△EOC∽△AOP,根据相似的性质得到∠OCE=∠OPA=90°,然后根据切线的判定定理得到DE是⊙O的切线;(3)根据平行线的性质由BC∥EP得到∠DCB=∠E,则tan∠DCB=tan∠E= ![]() ,在Rt△BCD中,根据正切的定义计算出BD=3,根据勾股定理计算出CD=
,在Rt△BCD中,根据正切的定义计算出BD=3,根据勾股定理计算出CD= ![]() ,然后根据平行线分线段成比例定理得
,然后根据平行线分线段成比例定理得 ![]() =
= ![]() ,再利用比例性质可计算出DE=
,再利用比例性质可计算出DE= ![]() .
.

【题目】七(1)班小明同学通过《测量硬币的厚度与质量》实验得到了每枚硬币的厚度和质量,数据如下表.他从储蓄罐取出一把5角和1元硬币,为了知道总的金额,他把这些硬币叠起来,用尺量出它们的总厚度为22.6mm,又用天平称出总质量为78.5g,请你帮助小明同学算出这把硬币的总金额为______元.
1元硬币 | 5角硬币 | |
每枚厚度(单位:mm) | 1.8 | 1.7 |
每枚质量(单位:g) | 6.1 | 6.0 |