题目内容
 如图,给出下列四组条件:
如图,给出下列四组条件:①AB=DE,BE=CF,AC=DF;②AB=DE,∠A=∠D,BC=EF;
③∠B=∠DEF,BE=CF,∠ACB=∠F;④AB∥DE,AC∥DF,∠A=∠D
其中,能使△ABC≌△DEF的条件共有( )
分析:根据全等三角形的判定定理结合所给条件分析证明△ABC≌△DEF即可.
解答:解:①由BE=CF可得BC=EF,再有AB=DE,AC=DF可利用SSS证明△ABC≌△DEF;
②AB=DE,∠A=∠D,BC=EF不能证明△ABC≌△DEF;
③∠B=∠DEF,BE=CF,∠ACB=∠F可利用ASA定理证明△ABC≌△DEF;
④AB∥DE,AC∥DF,∠A=∠D不能证明△ABC≌△DEF;
故选:B.
②AB=DE,∠A=∠D,BC=EF不能证明△ABC≌△DEF;
③∠B=∠DEF,BE=CF,∠ACB=∠F可利用ASA定理证明△ABC≌△DEF;
④AB∥DE,AC∥DF,∠A=∠D不能证明△ABC≌△DEF;
故选:B.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 12、如图,给出下列四组条件:
12、如图,给出下列四组条件: 15、如图,给出下列四组条件:
15、如图,给出下列四组条件: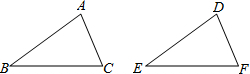 (2013•唐山一模)如图,给出下列四组条件:
(2013•唐山一模)如图,给出下列四组条件: 如图,给出下列四组条件:
如图,给出下列四组条件: 如图,给出下列四组条件:
如图,给出下列四组条件: