Question

【题目】如图，在平面直角坐标系中，矩形的边的边分别在轴，轴正半轴上，， 点从点出发以每秒2个单位长度的速度向终点运动，点不与点重合以为边在上方作正方形，设正方形与的重叠部分图形的面积为（平方单位），点的运动时间为（秒）．

（1）直线所在直线的解析式是__________________________．

（2）当点落在线段上时，求的值．

（3）在点运动的过程中，求与之间的函数关系式；

（4）设边的中点为，点关于点的对称点为，以为边在上方作正方形当正方形与重叠部分图形为三角形时，直接写出的取值范围．

（提示：根据点的运动，可在草纸上画出正方形与重叠部分图形为不同图形时的临界状态去研究．）

Answer 1

【答案】(1)； (2) ；(3)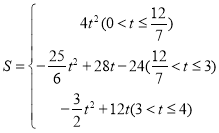 ；(4) 正方形KC′MN与△ABC重叠部分图形为三角形，t的取值范围为：和

【解析】

(1)根据OA=6，OC=8求出点A、C的坐标为(0，6)和(8，0)，用待定系数法可求得直线AC的解析式；
(2)点E在AC上时，四边形OIPEF是正方形得EP∥AO，可证明△CPE∽△COA，由相似三角形的性质即可求出t的值；
(3)点P运动过程中正方形OPEF与△ABC的重叠部分图形的形状不同，分3种情况考虑；
(4)根据点P的运动，先找出正方形KC′MN与△ABC重叠部分图形为三角形时的临界点，再综合求t的取值范围．

(1)设直线AC的解析式为，
如图1所示：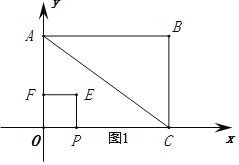

∵OA=6，OC=8，
∴点A、C的坐标分别为(0，6)，(8，0)，
将点A、C两点的坐标代入直线AC的解析式中得

，

解得：，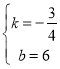

∴直线AC的解析式为：；

(2)当点E落在线段AC上时，如图2所示：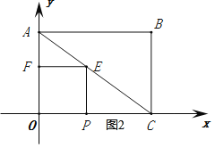

∵OC=8，P从点O出发以每秒2个单位长度的速度向点C运动，
∴，，，
∵EP∥AO，
∴△CPE∽△COA，

∴，即，

解得：；

(3)点P运动过程中正方形OPEF与△ABC的重叠部分图形的形状不同
分3种情况考虑，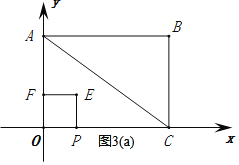

①当时，如图3(a)所示，
∵

∴；
②当时，如图3(b)所示，

∵，
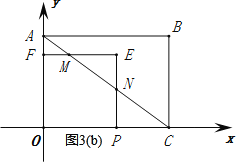
∴NP∥BC，FM∥AB，
∴△CNP∽△CAO∽△MAF，
∴，
∴，；
，
③当时，如图3(c)所示，

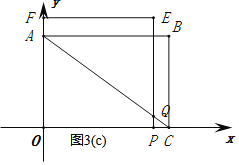
∵PQ∥AO，
∴△CPQ∽△COA，
∴，
∴，
=+12t；
(4)根据点P的运动，画出正方形KC′MN与△ABC重叠部分图形为三角形时的临界点，
①当P点开始向右移动时，正方形KC′MN与△ABC重叠部分图形为三角形，达到图4(a)所示情况不再为三角形，

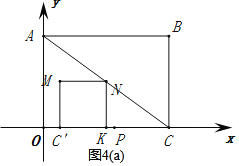
根据题意：KC'=KN，
∵点K为线段OC的中点，KN∥AO，
∴KN为△AOC的中位线，
∴KC'=KN=AO=×6=3，
CC'=KC'+KC=3+4=7，
∴，
解得：，
即；
②当点P运动到图4(b)所示情况时，正方形KC′MN与△ABC重叠部分图形开始为三角形．

∵，
∴，

∴，
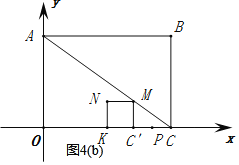
∴CC'=，MC'=，
∴，
解得：；
③当点P运动到图4(c)所示情况，正方形KC′MN与△ABC重叠部分图形为三角形，点P再运动到点C时不再为三角形．

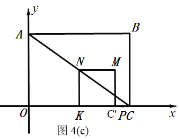
∵点K为线段OC的中点，KN∥AO，
∴KN为△AOC的中位线，
∴KC'=KN=AO＝3，CC'=KC-KC'，
∴PC=CC′=，
解得：，
综合所述：正方形KC′MN与△ABC重叠部分图形为三角形，t的取值范围为：和．