题目内容
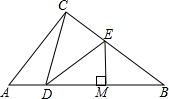 如图,在Rt△ACB中,∠ACB=90°,点D在边AB上,DE平分∠CDB交边BC于E,EM是线段BD的垂直平分线.
如图,在Rt△ACB中,∠ACB=90°,点D在边AB上,DE平分∠CDB交边BC于E,EM是线段BD的垂直平分线.
(1)求证: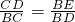 ;
;
(2)若AB=10,cosB= ,求CD的长.
,求CD的长.
(1)证明:∵EM是线段BD的垂直平分线,
∴ED=EB,
∴∠EDB=∠B,
∵DE平分∠CDB,
∴∠CDE=∠EDB,
∴∠CDE=∠B,
∵∠DCE=∠BCD,
∴△CDE∽△CBD,
∴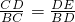 ,
,
∵ED=EB,
∴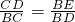 ;
;
(2)解:∵∠ACB=90°,AB=10,cosB= ,
,
∴AC=6,BC=8,
∵EM是线段BD的垂直平分线,
∴DM=BM,
∴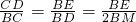 ,
,
∴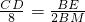 ,
,
即CD=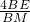 ,
,
∵cosB=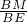 =
= ,
,
∴CD=4× =5.
=5.
分析:(1)由EM是线段BD的垂直平分线,可证得∠EDB=∠B,又由DE平分∠CDB,可证得∠CDE=∠B,继而可证得△CDE∽△CBD,然后由相似三角形的对应边成比例,证得结论;
(2)由∠ACB=90°,AB=10,cosB= ,可求得AC=6,BC=8,又由
,可求得AC=6,BC=8,又由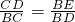 ,则可求得CD=
,则可求得CD=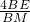 ,继而求得答案.
,继而求得答案.
点评:此题考查了相似三角形的判定与性质、线段垂直平分线的性质、角平分线的定义以及三角函数等知识.此题难度适中,注意掌握数形结合思想与转化思想的应用.
∴ED=EB,
∴∠EDB=∠B,
∵DE平分∠CDB,
∴∠CDE=∠EDB,
∴∠CDE=∠B,
∵∠DCE=∠BCD,
∴△CDE∽△CBD,
∴
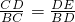 ,
,∵ED=EB,
∴
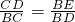 ;
;(2)解:∵∠ACB=90°,AB=10,cosB=
 ,
,∴AC=6,BC=8,
∵EM是线段BD的垂直平分线,
∴DM=BM,
∴
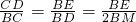 ,
,∴
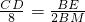 ,
,即CD=
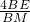 ,
,∵cosB=
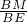 =
= ,
,∴CD=4×
 =5.
=5.分析:(1)由EM是线段BD的垂直平分线,可证得∠EDB=∠B,又由DE平分∠CDB,可证得∠CDE=∠B,继而可证得△CDE∽△CBD,然后由相似三角形的对应边成比例,证得结论;
(2)由∠ACB=90°,AB=10,cosB=
 ,可求得AC=6,BC=8,又由
,可求得AC=6,BC=8,又由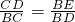 ,则可求得CD=
,则可求得CD=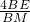 ,继而求得答案.
,继而求得答案.点评:此题考查了相似三角形的判定与性质、线段垂直平分线的性质、角平分线的定义以及三角函数等知识.此题难度适中,注意掌握数形结合思想与转化思想的应用.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
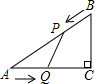 如图,在Rt△ACB中,∠C=90°AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为t(s)(0<t<2).根据以上信息,解答下列问题:
如图,在Rt△ACB中,∠C=90°AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为t(s)(0<t<2).根据以上信息,解答下列问题: 如图:在Rt△ACB中,∠C=90°,AC=8,BC=6,CD是斜边AB上的高.若点P在线段DB上,连接CP,sin∠APC=
如图:在Rt△ACB中,∠C=90°,AC=8,BC=6,CD是斜边AB上的高.若点P在线段DB上,连接CP,sin∠APC= 如图,在Rt△ACB中,∠C=90゜,点O为AB的中点,OE⊥OF交AC于E点、交BC于F点,EM⊥AB,FN⊥AB,垂足分别为M、N,
如图,在Rt△ACB中,∠C=90゜,点O为AB的中点,OE⊥OF交AC于E点、交BC于F点,EM⊥AB,FN⊥AB,垂足分别为M、N, 如图,在Rt△ACB中,∠C=90°,BE平分∠CBA交AC于点E,过E作ED⊥AB于D点,当∠A=
如图,在Rt△ACB中,∠C=90°,BE平分∠CBA交AC于点E,过E作ED⊥AB于D点,当∠A= 如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点,将Rt△ABC沿CD折叠,使点B落在AC边上的B′处,则∠ADB′等于
如图,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB上一点,将Rt△ABC沿CD折叠,使点B落在AC边上的B′处,则∠ADB′等于