题目内容
如图所示,四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=-| 1 | 2 |
(1)记△ODE的面积为S,求S与b的函数关系式;
(2)当点E在线段OA上时,若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1,试探究
 O1A1B1C1与矩形OABC的重叠部分的面积是否发生变化?若不变,求出该重叠部分的面积;若改变,请说明理由.
O1A1B1C1与矩形OABC的重叠部分的面积是否发生变化?若不变,求出该重叠部分的面积;若改变,请说明理由.
分析:(1)要表示出△ODE的面积,要分两种情况讨论,①如果点E在OA边上,只需求出这个三角形的底边OE长(E点横坐标)和高(D点纵坐标),代入三角形面积公式即可;②如果点E在AB边上,这时△ODE的面积可用长方形OABC的面积减去△OCD、△OAE、△BDE的面积;
(2)重叠部分是一个平行四边形,由于这个平行四边形上下边上的高不变,因此决定重叠部分面积是否变化的因素就是看这个平行四边形落在OA边上的线段长度是否变化.
(2)重叠部分是一个平行四边形,由于这个平行四边形上下边上的高不变,因此决定重叠部分面积是否变化的因素就是看这个平行四边形落在OA边上的线段长度是否变化.
解答: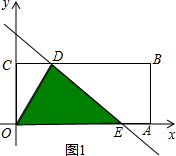 解:(1)∵四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1),
解:(1)∵四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1),
∴B(3,1),
若直线经过点A(3,0)时,则b=
若直线经过点B(3,1)时,则b=
若直线经过点C(0,1)时,则b=1
①若直线与折线OAB的交点在OA上时,即1<b≤
,如图1,
此时E(2b,0)
∴S=
OE•CO=
×2b×1=b;
②若直线与折线OAB的交点在BA上时,即
<b<
,如图2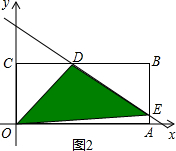
此时E(3,b-
),D(2b-2,1),
∴S=S矩-(S△OCD+S△OAE+S△DBE)
=3-[
(2b-2)×1+
×(5-2b)•(
-b)+
×3(b-
)]
=
b-b2,
∴S=
;
(2)如图3,设O1A1与CB相交于点M,OA与C1B1相交于点N,则矩形O1A1B1C1与矩形OABC的重叠部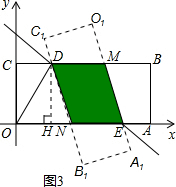 分的面积即为四边形DNEM的面积.
分的面积即为四边形DNEM的面积.
由题意知,DM∥NE,DN∥ME,
∴四边形DNEM为平行四边形
根据轴对称知,∠MED=∠NED
又∵∠MDE=∠NED,
∴∠MED=∠MDE,
∴MD=ME,
∴平行四边形DNEM为菱形.
过点D作DH⊥OA,垂足为H,设菱形DNEM的边长为a,
由题意知,D(2b-2,1),E(2b,0),
∴DH=1,HE=2b-(2b-2)=2,
∴HN=HE-NE=2-a,
则在Rt△DHN中,由勾股定理知:a2=(2-a)2+12,
∴a=
,
∴S四边形DNEM=NE•DH=
.
∴矩形OA1B1C1与矩形OABC的重叠部分的面积不发生变化,面积始终为
.
 解:(1)∵四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1),
解:(1)∵四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1),∴B(3,1),
若直线经过点A(3,0)时,则b=
| 3 |
| 2 |
若直线经过点B(3,1)时,则b=
| 5 |
| 2 |
若直线经过点C(0,1)时,则b=1
①若直线与折线OAB的交点在OA上时,即1<b≤
| 3 |
| 2 |
此时E(2b,0)
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
②若直线与折线OAB的交点在BA上时,即
| 3 |
| 2 |
| 5 |
| 2 |

此时E(3,b-
| 3 |
| 2 |
∴S=S矩-(S△OCD+S△OAE+S△DBE)
=3-[
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
=
| 5 |
| 2 |
∴S=
|
(2)如图3,设O1A1与CB相交于点M,OA与C1B1相交于点N,则矩形O1A1B1C1与矩形OABC的重叠部
 分的面积即为四边形DNEM的面积.
分的面积即为四边形DNEM的面积.由题意知,DM∥NE,DN∥ME,
∴四边形DNEM为平行四边形
根据轴对称知,∠MED=∠NED
又∵∠MDE=∠NED,
∴∠MED=∠MDE,
∴MD=ME,
∴平行四边形DNEM为菱形.
过点D作DH⊥OA,垂足为H,设菱形DNEM的边长为a,
由题意知,D(2b-2,1),E(2b,0),
∴DH=1,HE=2b-(2b-2)=2,
∴HN=HE-NE=2-a,
则在Rt△DHN中,由勾股定理知:a2=(2-a)2+12,
∴a=
| 5 |
| 4 |
∴S四边形DNEM=NE•DH=
| 5 |
| 4 |
∴矩形OA1B1C1与矩形OABC的重叠部分的面积不发生变化,面积始终为
| 5 |
| 4 |
点评:本题是一个动态图形中的面积是否变化的问题,看一个图形的面积是否变化,关键是看决定这个面积的几个量是否变化,本题题型新颖,是个不可多得的好题,有利于培养学生的思维能力,但难度较大,具有明显的区分度.

练习册系列答案
相关题目
 如图所示,四边形OABC为正方形,边长为6,点A,C分别在x轴,y轴的正半轴上,点D在OA上,且D的坐标为(2,0),P是OB上的一动点,试求PD+PA和的最小值是( )
如图所示,四边形OABC为正方形,边长为6,点A,C分别在x轴,y轴的正半轴上,点D在OA上,且D的坐标为(2,0),P是OB上的一动点,试求PD+PA和的最小值是( ) (2013•吴中区一模)如图所示,四边形OABC是矩形,点A、C的坐标分别为(6,0),(0,2),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=-
(2013•吴中区一模)如图所示,四边形OABC是矩形,点A、C的坐标分别为(6,0),(0,2),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=-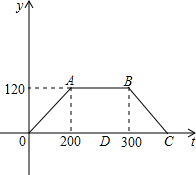 小明参加汽车驾驶培训,在实际操作考试时,被要求进行启动加速、匀速运行、制动减速三个连贯过程,在加速和减速运动过程中,路程和速度均满足关系s=
小明参加汽车驾驶培训,在实际操作考试时,被要求进行启动加速、匀速运行、制动减速三个连贯过程,在加速和减速运动过程中,路程和速度均满足关系s= 如图所示,四边形ABCD与A′B′C′D′以0为位似中心,位似比为1:2.则点A的对应点是点
如图所示,四边形ABCD与A′B′C′D′以0为位似中心,位似比为1:2.则点A的对应点是点