题目内容
【题目】如图,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,且
,且![]() .
.
![]() 求直线
求直线![]() 的解析式;
的解析式;
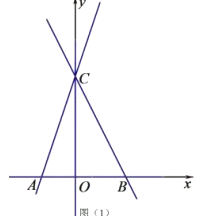
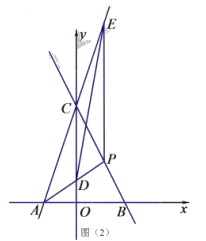
![]() 点
点![]() 在线段
在线段![]() 上,连接
上,连接![]() 交
交![]() 轴于点,过点
轴于点,过点![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() ,设点
,设点![]() 的坐标为
的坐标为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式(不要求写自变量的取值范围).
的函数关系式(不要求写自变量的取值范围).
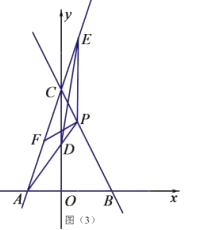
![]() 在
在![]() 的条件下,点
的条件下,点![]() 是线段
是线段![]() 上一点,连接
上一点,连接![]() ,当
,当![]() 时,且
时,且![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据题意先求出点B和点C的坐标,然后代入即可求得一次函数的解析式;
(2)过点![]() 作
作![]() 轴于
轴于![]() ,过
,过![]() 点作
点作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,根据题意求出EP,然后根据三角形的面积公式即可求出S与m的关系式;
,根据题意求出EP,然后根据三角形的面积公式即可求出S与m的关系式;
(3)根据题意先求出m,然后得到点P的坐标,延长![]() 交
交![]() 轴于
轴于![]() ,由
,由![]() 和三角形的外角和定理可得
和三角形的外角和定理可得![]() ,延长
,延长![]() 交
交![]() 轴于点
轴于点![]() ,由勾股定理和等腰三角形的性质可求得点M的坐标,从而求得PF所在直线的函数解析式,再根据求二元一次方程组的解得到交点F的坐标.
,由勾股定理和等腰三角形的性质可求得点M的坐标,从而求得PF所在直线的函数解析式,再根据求二元一次方程组的解得到交点F的坐标.
![]() 设直线
设直线![]() 的解析式是
的解析式是![]() ,
,
∵y=3x+6交y轴于点C,
∴当![]() 时,
时,![]() ,
,
![]() C(0,6),
C(0,6),
![]() ,
,![]()
![]() .
.
![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() ;
;
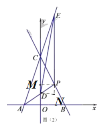
![]() 过点
过点![]() 作
作![]() 轴于
轴于![]() ,过
,过![]() 点作
点作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,如图所示:
,如图所示:
![]() 轴,
轴,![]() 轴,
轴,![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() 点的横坐标为
点的横坐标为![]() ,
,![]() ,
,
当![]() 时,
时,![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
,![]() 舍去,
舍去,![]() ,
,
![]() ,
,
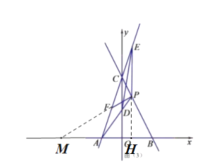
延长![]() 交
交![]() 轴于
轴于![]() ,
,![]() ,
,![]() ,
,![]() 轴,延长
轴,延长![]() 交
交![]() 轴于点
轴于点![]() ,
,
如图所示:
![]() ,
,![]() ,
,![]() ,
,![]() .
.![]() ,
,![]()
![]() 直线
直线![]() 的解析式为
的解析式为![]() ,
,
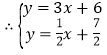 ,解得
,解得![]() ,
,![]() .
.

练习册系列答案
相关题目