题目内容
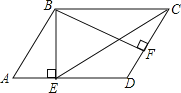
【题目】如图，四边形ABCD中，AD平行BC，∠ABC=90°，AD=2，AB=6，以AB为直径的半⊙O 切CD于点E，F为弧BE上一动点，过F点的直线MN为半⊙O的切线，MN交BC于M，交CD于N，则△MCN的周长为（ ）
A.9 B.10 C.3
D.2
【答案】A
【解析】
试题分析：作DH⊥BC于H，如图，利用平行线的性质得AB⊥AD，AB⊥BC，则根据切线的判定得到AD和BC为⊙O切线，根据切线长定理得DE=DA=2，CE=CB，NE=NF，MB=MF，利用四边形ABHD为矩形得BH=AD=2，DH=AB=6，设BC=x，则CH=x﹣2，CD=x+2，在Rt△DCH中根据勾股定理得（x﹣2）2+62=（x+2）2，解得x=
，即CB=CE=，然后由等线段代换得到△MCN的周长=CE+CB=9．
故选A．
练习册系列答案
相关题目
