Question

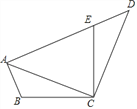
【题目】如图，在△ABC中，已知AC=BC=5，AB=6，点E是线段AB上的动点（不与端点重合），点F是线段AC上的动点，连接CE、EF，若在点E、点F的运动过程中，始终保证∠CEF=∠B．当以点C为圆心，以CF为半径的圆与AB相切时，则BE的长为_________．

Answer 1

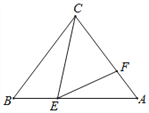
【答案】1或5

【解析】如图，设⊙C与BA切于点M，则CM=CF，CM⊥BA，根据等腰三角形的三线合一的性质可得BM=AM==3，在Rt△AMC中，根据勾股定理求得CM=CF= 4，从而得AF=1，再证明△AEF∽△BCE，根据相似三角形的性质可得，设BE长为x，则EA长为6-x，可得，解方程求得x的值，即可得BE的长.

如图，设⊙C与BA切于点M，则CM=CF，CM⊥BA，

∵CA=CB，CM⊥BA，AB=6，

∴BM=AM==3，

Rt△AMC中，AC=5，AM=3，

∴CM=CF= 4，

∴AF=1，

∵CA=CB，

∴∠B=∠A，

∵∠B+∠BCE=∠CEA=∠CEF+∠FEA，

∵∠CEF=∠B，

∴∠AEF=∠BCE；

∴△AEF∽△BCE，

∴ ，

设BE长为x，则EA长为6-x

∴，

解得：x1=1，x2=5，

∴BE的长为1或5.

故答案为：1或5.