题目内容
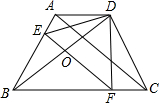 等腰梯形ABCD中,AD∥BC,AB=DC,折叠梯形ABCD,使点B与点D重合,EF为折痕,且DF⊥BC,下列结论:
等腰梯形ABCD中,AD∥BC,AB=DC,折叠梯形ABCD,使点B与点D重合,EF为折痕,且DF⊥BC,下列结论:
①△BFD为等腰直角三角形;②△ABD∽△ADE;③EF∥AC;④AD+FC>DF
其中正确的是
- A.②④
- B.①④
- C.②③
- D.①③
D
分析:根据等腰梯形及折叠的性质对条件进行判断即可.
解答: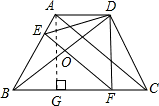 解:由折叠的性质知:EF垂直平分BD;
解:由折叠的性质知:EF垂直平分BD;
∴EF⊥BD,BF=DF;
又∵DF⊥BF,
∴△BDF是等腰直角三角形;故①正确;
∴∠DBF=45°;
易证得△DBC≌△ACB,得∠ACB=∠DBC=45°;
∴∠BNC=90°;
∴EF∥AC;故③正确;
过A作AG⊥BC,则BG=FC;
∴DF=BF=BG+GF=AD+FC;故④错误;
若②成立,则∠AED=∠BDA,∠ADE=∠ABD;
由折叠的性质知:∠ABD=∠EDB,
∴∠ADE=∠BDE,即DE平分∠ADB;
由于没有条件能直接证明DE是∠ADB的平分线,故②不一定成立;
所以正确的结论是①③,故选D.
点评:此题主要考查的是等腰梯形的性质、折叠的性质、相似三角形的判定等知识.
分析:根据等腰梯形及折叠的性质对条件进行判断即可.
解答:
 解:由折叠的性质知:EF垂直平分BD;
解:由折叠的性质知:EF垂直平分BD;∴EF⊥BD,BF=DF;
又∵DF⊥BF,
∴△BDF是等腰直角三角形;故①正确;
∴∠DBF=45°;
易证得△DBC≌△ACB,得∠ACB=∠DBC=45°;
∴∠BNC=90°;
∴EF∥AC;故③正确;
过A作AG⊥BC,则BG=FC;
∴DF=BF=BG+GF=AD+FC;故④错误;
若②成立,则∠AED=∠BDA,∠ADE=∠ABD;
由折叠的性质知:∠ABD=∠EDB,
∴∠ADE=∠BDE,即DE平分∠ADB;
由于没有条件能直接证明DE是∠ADB的平分线,故②不一定成立;
所以正确的结论是①③,故选D.
点评:此题主要考查的是等腰梯形的性质、折叠的性质、相似三角形的判定等知识.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

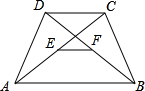 如图,在等腰梯形ABCD中,AB∥CD,∠ABC=60°,AC平分∠DAB,E、F分别为对角线AC、DB的中点,且EF=4.求这个梯形的面积.
如图,在等腰梯形ABCD中,AB∥CD,∠ABC=60°,AC平分∠DAB,E、F分别为对角线AC、DB的中点,且EF=4.求这个梯形的面积. (1)如图,在等腰梯形ABCD中,AD∥BC,AB∥DE,BC=8,AD=5,求EC的长.
(1)如图,在等腰梯形ABCD中,AD∥BC,AB∥DE,BC=8,AD=5,求EC的长.
 在等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠C=60°,
在等腰梯形ABCD中,AD∥BC,BD平分∠ABC,∠C=60°, 等腰梯形ABCD中,AD=2,BC=4,高DF=2,则腰CD长是
等腰梯形ABCD中,AD=2,BC=4,高DF=2,则腰CD长是