Question

【题目】（1）如图1，△ABC中，，AB的垂直平分线交AC于点D，连接BD．若AC=2，BC=1，则△BCD的周长为 ；

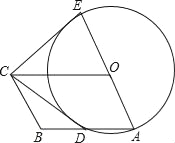
（2）O为正方形ABCD的中心，E为CD边上一点，F为AD边上一点，且△EDF的周长等于AD的长．

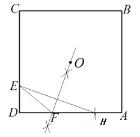
①在图2中求作△EDF（要求：尺规作图，不写作法，保留作图痕迹）；

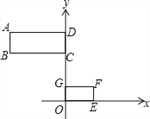
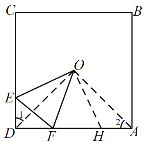
②在图3中补全图形，求的度数；

③若，则的值为 ．

Answer 1

【答案】（1）3（2）①图形见解析②45°③．

【解析】

试题分析：（1）利用垂直平分线的性质将△BCD的周长转化为BC+AC的长；（2）①在AD上截取AH，使得AH=DE，连接EH,作线段EH的垂直平分线交AD于F，连结EF可得所求的△EDF；②在AD上截取AH，使得AH=DE，连接OA、OD、OH．根据条件证明△≌△和△≌△．从而得出；③结合②中的结论，构造相似三角形，利用相似三角形的性质可得出结论．

试题解析：（1）；

（2）①如图，△即为所求；

②在AD上截取AH，使得AH=DE，连接OA、OD、OH．

∵点O为正方形ABCD的中心，

∴，，．

∴△≌△．

∴，．

∴．

∵△的周长等于的长，

∴．

∴△≌△．

∴．

③．