题目内容
 在直角梯形ABCD中,AB∥CD,∠B=90°,AB=4,BC=DC=3,P为梯形ABCD边上的一个动点,它从点A出发,沿A→B→C→D运动.若设点P经过的路程为x,△APC的面积为S.则当x等于多少时,△APC的面积S=3?(如答案有多样,可根据需要,自行画图,并解答)
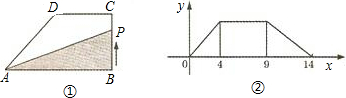
在直角梯形ABCD中,AB∥CD,∠B=90°,AB=4,BC=DC=3,P为梯形ABCD边上的一个动点,它从点A出发,沿A→B→C→D运动.若设点P经过的路程为x,△APC的面积为S.则当x等于多少时,△APC的面积S=3?(如答案有多样,可根据需要,自行画图,并解答)
 解:①如图1,当点P在AB边上时,S△APC=
解:①如图1,当点P在AB边上时,S△APC= AP•BC=
AP•BC= •x×3=3,
•x×3=3,解得x=2,即当x=2时,△APC的面积S=3;
②如图2,当点P在BC边上时,S△APC=
 PC•AB=
PC•AB= •(7-x)×4=3,
•(7-x)×4=3,解得x=
 ,即当x=
,即当x= 时,△APC的面积S=3;
时,△APC的面积S=3;③如图,当点P在CD边上时,S△APC=
 PD•BC=
PD•BC= •(10-x)×3=3,
•(10-x)×3=3,解得x=8,即当x=8时,△APC的面积S=3;
综上所述,当x的值为2,
 ,8时,△APC的面积S=3.
,8时,△APC的面积S=3.分析:需要分类讨论:当点P在AB边上,点P在BC边上,点P在CD边上.
点评:本题考查了动点函数图象.对于动点问题,需要分类讨论,以防漏解或错解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
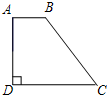 如图,在直角梯形ABCD中,AB∥DC,∠D=90°,若AD=8,BC=10,则cosC的值为( )
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,若AD=8,BC=10,则cosC的值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,且AB=BC=4AD,E是AB上的一点,DE⊥EC.求证:CE平分∠BCD.
如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,且AB=BC=4AD,E是AB上的一点,DE⊥EC.求证:CE平分∠BCD. 如图,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿过点D的直线折叠,使点A刚好落在BC边上,则此时折痕的长为
如图,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿过点D的直线折叠,使点A刚好落在BC边上,则此时折痕的长为 如图,在直角梯形ABCD中,若AD=5,点A的坐标为(-2,7),则点D的坐标为( )
如图,在直角梯形ABCD中,若AD=5,点A的坐标为(-2,7),则点D的坐标为( )