题目内容
已知△ABC中,AC=BC,∠CAB=α(定值),圆O的圆心O在AB上,并分别与AC、BC相切于点P、Q.(1)求∠POQ的大小(用α表示);
(2)设D是CA延长线上的一个动点,DE与圆O相切于点M,点E在CB的延长线上,试判断∠DOE的大小是否保持不变,并说明理由;
(3)在(2)的条件下,如果AB=m(m为已知数),cosα=
| 3 | 5 |
 关于x的函数解析式(要指出函数的定义域)
关于x的函数解析式(要指出函数的定义域)
分析:(1)根据题意得∠OAP=∠OBQ=α,再由圆O分别和AC、BC相切,推得∠POQ=2α;
(2)先证明△OEM≌△OEQ,得出两对相等的角:∠MOE=∠QOE,∠MOD=∠POD,则∠DOE=180°-a,从而得出结论∠DOE的大小保持不变.
(3)由三角函数的定义,求出AP,DM的长,然后证明△ADO∽△BOE,得出比例式
=
,求得BE、ME,表示出DE=DM+ME=x+
+
m,写出所求的函数解析为y=x+
+
m(x>0).
(2)先证明△OEM≌△OEQ,得出两对相等的角:∠MOE=∠QOE,∠MOD=∠POD,则∠DOE=180°-a,从而得出结论∠DOE的大小保持不变.
(3)由三角函数的定义,求出AP,DM的长,然后证明△ADO∽△BOE,得出比例式
| BE |
| AO |
| AD |
| BO |
| m2 |
| 4x |
| 3 |
| 5 |
| m2 |
| 4x |
| 3 |
| 5 |
解答:解:(1)∵AC=BC,
∴∠OAP=∠OBQ=α
∵圆O分别和AC、BC相切于点P、Q,
∴∠OPA=∠OQB=90°,(1分)
∴∠AOP=∠BOQ=90°-α(1分)
∴∠POQ=180°-2(90°-a)=2α(1分)
(2)∠DOE的大小保持不变,(1分)
说明理由如下:
连接OM,由切线长定理,EM=EQ
又∵OM=OQ,OE=OE,
∴△OEM≌△OEQ,
∴∠MOE=∠QOE(1分)
同理,∠MOD=∠POD(1分)
∴∠DOE=
(∠POM+∠QOM)=
(360°-∠POQ)=180°-a,
∵a为定值,
∴∠DOE的大小保持不变.
(3)由OP=OQ,并根据等腰三角形的性质,得O是AB的中点,
即OA=OB=
AB=
,
AP=BQ=AO•cosa=
m,DM=DP=
m+x(1分)
在△ADO和△BOE中,∠DAO=∠OBE=180°-α
∵∠ADO+∠AOD=∠OAP=α,
又∵∠BOE+∠AOD=180°-∠DOE=α,
∴∠ADO=∠BOE,于是△ADO∽△BOE(1分)
∴
=
,BE=
=
(1分)
∴ME=QE=QB+BE=
m+
(1分)
∴DE=DM+ME=
m+x+
m+
=x+
+
m
因此所求的函数解析为y=x+
+
m(x>0).(1分)
∴∠OAP=∠OBQ=α
∵圆O分别和AC、BC相切于点P、Q,
∴∠OPA=∠OQB=90°,(1分)
∴∠AOP=∠BOQ=90°-α(1分)

∴∠POQ=180°-2(90°-a)=2α(1分)
(2)∠DOE的大小保持不变,(1分)
说明理由如下:
连接OM,由切线长定理,EM=EQ
又∵OM=OQ,OE=OE,
∴△OEM≌△OEQ,
∴∠MOE=∠QOE(1分)
同理,∠MOD=∠POD(1分)
∴∠DOE=
| 1 |
| 2 |
| 1 |
| 2 |
∵a为定值,
∴∠DOE的大小保持不变.
(3)由OP=OQ,并根据等腰三角形的性质,得O是AB的中点,
即OA=OB=
| 1 |
| 2 |
| m |
| 2 |
AP=BQ=AO•cosa=
| 3 |
| 10 |
| 3 |
| 10 |
在△ADO和△BOE中,∠DAO=∠OBE=180°-α
∵∠ADO+∠AOD=∠OAP=α,
又∵∠BOE+∠AOD=180°-∠DOE=α,
∴∠ADO=∠BOE,于是△ADO∽△BOE(1分)
∴
| BE |
| AO |
| AD |
| BO |
| AO•BO |
| AD |
| m2 |
| 4x |
∴ME=QE=QB+BE=
| 3 |
| 10 |
| m2 |
| 4x |
∴DE=DM+ME=
| 3 |
| 10 |
| 3 |
| 10 |
| m2 |
| 4x |
| m2 |
| 4x |
| 3 |
| 5 |
因此所求的函数解析为y=x+
| m2 |
| 4x |
| 3 |
| 5 |
点评:此题作为压轴题,综合考查函数、方程与圆的切线,三角形相似的判定与性质等知识.难度较大,有利于培养同学们的钻研精神和坚韧不拔的意志品质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 12、已知△ABC中,AC=BC,∠C=Rt∠.如图,将△ABC进行折叠,使点A落在线段BC上(包括点B和点C),设点A的落点为D,折痕为EF,当△DEF是等腰三角形时,点D可能的位置共有( )
12、已知△ABC中,AC=BC,∠C=Rt∠.如图,将△ABC进行折叠,使点A落在线段BC上(包括点B和点C),设点A的落点为D,折痕为EF,当△DEF是等腰三角形时,点D可能的位置共有( ) 如图:已知△ABC中,AC=BC,∠ACB=90°,直角∠DFE的顶点F是AB中点,两边FD、FE分别交AC,BC于点D,E两点,给出以下个结论:
如图:已知△ABC中,AC=BC,∠ACB=90°,直角∠DFE的顶点F是AB中点,两边FD、FE分别交AC,BC于点D,E两点,给出以下个结论: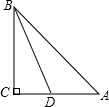 如图,已知△ABC中,AC=BC,∠ACB=90°,BD平分∠ABC,求证:AB=BC+CD.
如图,已知△ABC中,AC=BC,∠ACB=90°,BD平分∠ABC,求证:AB=BC+CD. 已知△ABC中,AC=BC,AD平分∠BAC交BC于D,点E为AB上一点,且∠EDB=∠B,现有下列两个结论:①AB=AD+CD ②AB=AC+CD.
已知△ABC中,AC=BC,AD平分∠BAC交BC于D,点E为AB上一点,且∠EDB=∠B,现有下列两个结论:①AB=AD+CD ②AB=AC+CD.