题目内容
如图,抛物线y=ax2+bx- 交x轴于A(-3,0)、B(1,0)两点,交y轴于点C,点D在抛物线上,且CD∥AB,对称轴直线l交x轴于点M,连结CM,将∠CMB绕点M旋转,旋转后的两边分别交直线BC、直线CD于点E、F.
交x轴于A(-3,0)、B(1,0)两点,交y轴于点C,点D在抛物线上,且CD∥AB,对称轴直线l交x轴于点M,连结CM,将∠CMB绕点M旋转,旋转后的两边分别交直线BC、直线CD于点E、F.
(1)求抛物线的解析式;
(2)当点E为BC中点时,射线MF与抛物线的交点坐标是______;
(3)若ME= CF,求点E的坐标.
CF,求点E的坐标.
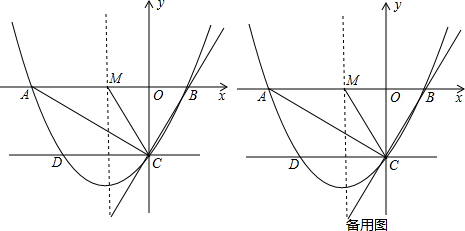
解:(1)因为抛物线过A(-3,0)、B(1,0)两点,
∴ ,
,
解得: ,
,
∴ ;
;
(2)∵OB=1,BC=2,
∴∠BCO=30°,
∴∠CBO=60°,
∴△MBC是等边三角形,
∴∠CMB=60°,
∴∠BMC=∠EMF=60°,
当点E为BC中点时,
∴∠BME=∠CME=30°,
∴∠FMC=30°,
∴MF是抛物线的对称轴,
∴射线MF与抛物线的交点是抛物线的顶点,
∵ ,
,
∴顶点坐标为: ,
,
(3)∵OA=3,OB=1,OC= ,
,
∴ ,
,
又∠AOC=∠BOC=90°,
∴△AOC∽△COB,
∴∠OAC=∠BCO,
∴∠ACB=90°,
∵M为AB中点,
∴CM=BM,
∵OB=1,BC=2,
∴∠BCO=30°,
∴∠CBO=60°,
∴△MBC是等边三角形,
∴∠CMB=∠MCB=60°,
∵AB∥CD,
∴∠ACD=30°,
∴∠BCD=120°,
∴∠BCD+∠EMF=180°,
∴∠MEC+∠MFC=180°,
∴∠MEB=∠MFC,
又∵∠EMB=∠CMF,
∴ ,
,
∴△MBE≌△MCF,
∴MF=ME,
又∵ME= CF,
CF,
∴MF= CF,
CF,
令对称轴与CD交于点H,点F的横坐标为t,
在直角△MHF中MF2=MH2+HF2
即 ,
,
∴ ,
, ,
,
当 时,BE=CF=
时,BE=CF= ,
,
过点E作EG⊥x轴,垂足为G,
在直角△BGE中,
∵∠GBE=60°,
∴∠GEB=30°,
∴GB=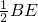 =
= ,
,
∴GE= ,
,
∴E( ,
,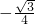 ),
),
同理,当 时,点E(
时,点E( ,
, ).
).
故答案为: .
.
分析:(1)把A(-3,0)、B(1,0)两点的坐标分别代入抛物线y=ax2+bx- 求出a和b的值即可得到抛物线的解析式;
求出a和b的值即可得到抛物线的解析式;
(2)根据旋转的性质可知∠BMC=∠EMF,再根据题目的已知条件可证明△BMC是等边三角形,所以∠BMC=∠EMF=60°,由等边三角形的性质可求出F点的坐标,当点E为BC中点时,可以证明射线MF与抛物线的交点恰好是抛物线的顶点;
(3)由(2)可知△MBC是等边三角形,所以∠CMB=∠MCB=60°,因为AB∥CD,所以∠ACD=30°,所以∠BCD=120°,所以∠BCD+∠EMF=180°,所以∠MEC+∠MFC=180°,进而得到∠MEB=∠MFC,又∠EMB=∠CMF,所以△MBE≌△MCF,所以MF=ME,又ME= CF,所以可得到MF=
CF,所以可得到MF= CF,令对称轴与CD交于点H,点F的横坐标为t,利用勾股定理计算即可.
CF,令对称轴与CD交于点H,点F的横坐标为t,利用勾股定理计算即可.
点评:本题综合性的考查了用待定系数法求抛物线的解析式、用公式法求抛物线的顶点坐标、等边三角形的判定和性质、直角三角形的判定和性质、勾股定理的运用、全等三角形的判定和性质以及相似三角形的判定和性质,题目的综合性很强.难度很大,对学生的解题能力要求较高.
∴
 ,
,解得:
 ,
,∴
 ;
;
(2)∵OB=1,BC=2,
∴∠BCO=30°,
∴∠CBO=60°,
∴△MBC是等边三角形,
∴∠CMB=60°,
∴∠BMC=∠EMF=60°,
当点E为BC中点时,
∴∠BME=∠CME=30°,
∴∠FMC=30°,
∴MF是抛物线的对称轴,
∴射线MF与抛物线的交点是抛物线的顶点,
∵
 ,
,∴顶点坐标为:
 ,
,(3)∵OA=3,OB=1,OC=
 ,
,∴
 ,
,又∠AOC=∠BOC=90°,
∴△AOC∽△COB,
∴∠OAC=∠BCO,
∴∠ACB=90°,
∵M为AB中点,
∴CM=BM,

∵OB=1,BC=2,
∴∠BCO=30°,
∴∠CBO=60°,
∴△MBC是等边三角形,
∴∠CMB=∠MCB=60°,
∵AB∥CD,
∴∠ACD=30°,
∴∠BCD=120°,
∴∠BCD+∠EMF=180°,
∴∠MEC+∠MFC=180°,
∴∠MEB=∠MFC,
又∵∠EMB=∠CMF,
∴
 ,
,∴△MBE≌△MCF,
∴MF=ME,
又∵ME=
 CF,
CF,∴MF=
 CF,
CF,令对称轴与CD交于点H,点F的横坐标为t,
在直角△MHF中MF2=MH2+HF2
即
 ,
,∴
 ,
, ,
,当
 时,BE=CF=
时,BE=CF= ,
,过点E作EG⊥x轴,垂足为G,
在直角△BGE中,
∵∠GBE=60°,
∴∠GEB=30°,
∴GB=
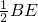 =
= ,
,∴GE=
 ,
,∴E(
 ,
,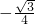 ),
),同理,当
 时,点E(
时,点E( ,
, ).
).故答案为:
 .
.分析:(1)把A(-3,0)、B(1,0)两点的坐标分别代入抛物线y=ax2+bx-
 求出a和b的值即可得到抛物线的解析式;
求出a和b的值即可得到抛物线的解析式;(2)根据旋转的性质可知∠BMC=∠EMF,再根据题目的已知条件可证明△BMC是等边三角形,所以∠BMC=∠EMF=60°,由等边三角形的性质可求出F点的坐标,当点E为BC中点时,可以证明射线MF与抛物线的交点恰好是抛物线的顶点;
(3)由(2)可知△MBC是等边三角形,所以∠CMB=∠MCB=60°,因为AB∥CD,所以∠ACD=30°,所以∠BCD=120°,所以∠BCD+∠EMF=180°,所以∠MEC+∠MFC=180°,进而得到∠MEB=∠MFC,又∠EMB=∠CMF,所以△MBE≌△MCF,所以MF=ME,又ME=
 CF,所以可得到MF=
CF,所以可得到MF= CF,令对称轴与CD交于点H,点F的横坐标为t,利用勾股定理计算即可.
CF,令对称轴与CD交于点H,点F的横坐标为t,利用勾股定理计算即可.点评:本题综合性的考查了用待定系数法求抛物线的解析式、用公式法求抛物线的顶点坐标、等边三角形的判定和性质、直角三角形的判定和性质、勾股定理的运用、全等三角形的判定和性质以及相似三角形的判定和性质,题目的综合性很强.难度很大,对学生的解题能力要求较高.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少? O为坐标原点,抛物线上一点C的横坐标为1.
O为坐标原点,抛物线上一点C的横坐标为1. 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12, 与x轴交于点A、B,点A的坐标为(-2,0).
与x轴交于点A、B,点A的坐标为(-2,0).