Question

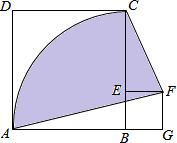（2013•烟台）如图，正方形ABCD的边长为4，点E在BC上，四边形EFGB也是正方形，以B为圆心，BA长为半径画

AC

，连结AF，CF，则图中阴影部分面积为

4π

．

Answer 1

分析：设正方形EFGB的边长为a，表示出CE、AG，然后根据阴影部分的面积=S_扇形ABC+S_{正方形EFGB}+S_△CEF-S_△AGF，列式计算即可得解．

解答：解：设正方形EFGB的边长为a，则CE=4-a，AG=4+a，
阴影部分的面积=S_扇形ABC+S_{正方形EFGB}+S_△CEF-S_△AGF
=

90•π•42

360

+a²+

1

2

a（4-a）-

1

2

a（4+a）
=4π+a²+2a-

1

2

a²-2a-

1

2

a²
=4π．
故答案为：4π．

点评：本题考查了正方形的性质，整式的混合运算，扇形的面积计算，引入小正方形的边长这一中间量是解题的关键．