题目内容
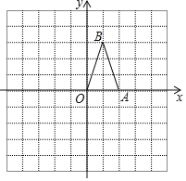
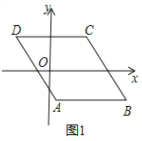
【题目】如图,在平面直角坐标系中,线段AB在x轴上点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.得平行四边形ABDC

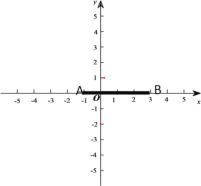
(1)补全图形,直接写出点C,D的坐标;
(2)若在y轴上存在点M,连接MA,MB,使S△MAB=S四边形ABDC,求出点M的坐标.
(3)若点P在直线BD上运动,连接PC,PO.请画出图形,探索∠CPO、∠DCP、∠BOP的数量关系并说明理由.
【答案】(1)![]() ,
,![]() ;详见解析;(2)
;详见解析;(2)![]() 点的坐标为
点的坐标为![]() 或
或![]() ;(3)详见解析,①当点
;(3)详见解析,①当点![]() 在
在![]() 上,
上,![]() ;②当点
;②当点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() ③当点
③当点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]()
【解析】
(1)根据平移法则作图即可,由平移法则可得出点C,D的坐标;
(2)求出![]() ,设
,设![]() 坐标为
坐标为![]() ,利用三角形面积公式列式求解即可;
,利用三角形面积公式列式求解即可;
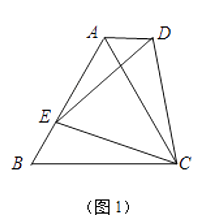
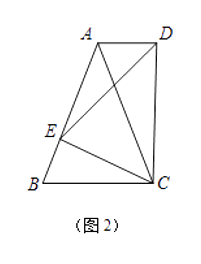
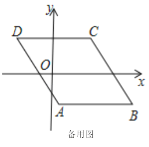
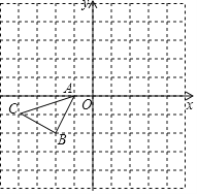
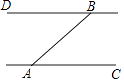
(3)分类讨论:当点P在BD上,如图1,作PE∥CD,根据平行线的性质得CD∥PE∥AB,则∠DCP=∠EPC,∠BOP=∠EPO,易得∠DCP+∠BOP=∠EPC+∠EPO=∠CPO;当点P在线段BD的延长线上时,如图2,同样有∠DCP=∠EPC,∠BOP=∠EPO,由于∠EPO-∠EPC=∠BOP-∠DCP,于是∠BOP-∠DCP=∠CPO;同理可得当点P在线段DB的延长线上时,∠DCP-∠BOP=∠CPO.
解:(1)如图,

∵将![]() ,
,![]() 分别向上平移2个单位,再向右平移1个单位,
分别向上平移2个单位,再向右平移1个单位,
∴![]() ,
,![]() ;
;
(2)∵![]() ,
,![]() ,
,
∴![]() ,
,
设![]() 坐标为
坐标为![]() ,
,
∴![]() ,解得
,解得![]()
∴![]() 点的坐标为
点的坐标为![]() 或
或![]() ;
;
(3)三种情况
①当点![]() 在
在![]() 上,如图1,
上,如图1,

由平移的性质得,![]() ,
,
过点![]() 作
作![]() ,则
,则![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
②当点![]() 在线段
在线段![]() 的延长线上时,如图2,
的延长线上时,如图2,

由平移的性质得,![]() ,
,
过点![]() 作
作![]() ,则
,则![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
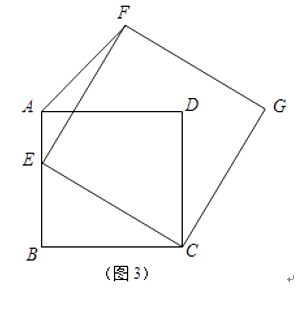
③当点![]() 在线段
在线段![]() 的延长线上时,如图3,
的延长线上时,如图3,

同(2)的方法得出![]()

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目