题目内容
如图85，三所学校分别记作A，B，C
．体育场记作O，它是△ABC的三条角平分线的交点．O，A，B，C每两地之间有直线道路相连．一支长跑队伍从体育场O点出发，跑遍各校再回到O点．指出哪条路线跑的距离最短（已知AC＞BC＞AB），并说明理由．
解：若不考虑顺序，所跑的路线有三条：
OABCO（或OCBAO），OACBO（或OBCAO），OBACO（或OCABO）．其中OABCO的距离最短．
记d(OABCO)，d(OACBO)，d(OBACO)分别为三条路线的距离．在AC上截取AB＇=AB，连结OB＇．则△ABO≌△AB＇O．∴BO=B＇O．
d(OABCO)-d(OACBO)
=(OA+AB+BC+CO)-(OA+AC+CB+BO)
=AB+CO-AC-BO
=AB+CO-AB＇-B＇C-B＇O
=CO-(B＇C+B＇O)＜0
同理可得，d(OABCO)-d(OBACO)＜0．
所以路线OABCO的距离最短．
练习册系列答案
相关题目
某初中学校欲向高一级学校推荐一名学生，根据规定的推荐程序：首先由本年级200名学生民主投票，每人只能推荐一人（不设弃权票），选出了票数最多的甲、乙、丙三人．投票结果统计如图一：
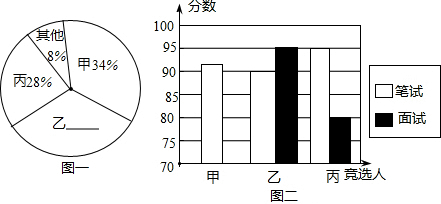
其次，对三名候选人进行了笔试和面试两项测试．各项成绩如下表所示：
图二是某同学根据上表绘制的一个不完全的条形图．
请你根据以上信息解答下列问题：
（1）补全图一和图二；
（2）请计算每名候选人的得票数；
（3）若每名候选人得一票记1分，投票、笔试、面试三项得分按照2：5：3的比确定，计算三名候选人的平均成绩，成绩高的将被录取，应该录取谁？
其次，对三名候选人进行了笔试和面试两项测试．各项成绩如下表所示：
| 测试项目 | 测试成绩/分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 92 | 90 | 95 |
| 面试 | 85 | 95 | 80 |
请你根据以上信息解答下列问题：
（1）补全图一和图二；
（2）请计算每名候选人的得票数；
（3）若每名候选人得一票记1分，投票、笔试、面试三项得分按照2：5：3的比确定，计算三名候选人的平均成绩，成绩高的将被录取，应该录取谁？
某中学有三名学生竞选学生会主席，他们的笔试成绩和口试成绩（单位：分）分别用了两种方式进行了统计，并绘制了不完整的成绩表和统计图1．
| 竞选人 | A | B | C |
| 笔试 | 85 | 95 | 90 |
| 口试 | 80 | 85 |
（1）请把图1空缺的部分补充完整；
（2）竞选的最后一个程序是由本校的300名学生进行投票，三位竞选人的得票情况如图2（没有弃权票，每名学生只能选举一人）所示，请计算竞选人A的得票数；
（3）在（2）条件下，若每票得1分，学校将笔试、口试、得票三项测试得分按2：4：4的比例确定每个人的成绩，请计算出竞选人B的最后成绩．
某初中学校欲向高一级学校推荐一名学生，根据规定的推荐程序：首先由本年级200名学生民主投票，每人只能推荐一人（不设弃权票），选出了票数最多的甲、乙、丙三人。图票结果统计如图一：
其次，对三名候选人进行了笔试和面试两项测试。各项成绩如下表所示：
| 测试项目 | 测试成绩/分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 92 | 90 | 95 |
| 面试 | 85 | 95 | 80 |
图二是某同学根据上表绘制的一个不完全的条形图。
请你根据以上信息解答下列问题：
（1）、补全图一和图二；
（2）、请计算每名候选人的得票数；
（3）、若每名候选人得一票记1分，投票、笔试、面试三项得分按照2：5：3的比确定，计算三名候选人的平均成绩，成绩高的将被录取，应该录取谁？
某中学有三名学生竞选学生会主席，他们的笔试成绩和口试成绩（单位：分）分别用了两种方式进行了统计，并绘制了不完整的成绩表和统计图1．
（1）请把图1空缺的部分补充完整；
（2）竞选的最后一个程序是由本校的300名学生进行投票，三位竞选人的得票情况如图2（没有弃权票，每名学生只能选举一人）所示，请计算竞选人A的得票数；
（3）在（2）条件下，若每票得1分，学校将笔试、口试、得票三项测试得分按2：4：4的比例确定每个人的成绩，请计算出竞选人B的最后成绩．
| 竞选人 | A | B | C |
| 笔试 | 85 | 95 | 90 |
| 口试 | 80 | 85 |
（1）请把图1空缺的部分补充完整；
（2）竞选的最后一个程序是由本校的300名学生进行投票，三位竞选人的得票情况如图2（没有弃权票，每名学生只能选举一人）所示，请计算竞选人A的得票数；
（3）在（2）条件下，若每票得1分，学校将笔试、口试、得票三项测试得分按2：4：4的比例确定每个人的成绩，请计算出竞选人B的最后成绩．