题目内容
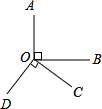如图，OA⊥OB，OC⊥OD．若∠AOD=144°，则∠BOC=36°
36°
．分析：根据垂直的定义知∠AOB=∠COD=90°，然后由周角的定义即可求得∠BOC的度数．
解答：解：∵OA⊥OB，OC⊥OD，
∴∠AOB=∠COD=90°；
又∵∠AOD+∠AOB+∠BOC+∠COD=360°，∠AOD=144°，
∴∠BOC=36°；
故答案是：36°．
∴∠AOB=∠COD=90°；
又∵∠AOD+∠AOB+∠BOC+∠COD=360°，∠AOD=144°，
∴∠BOC=36°；
故答案是：36°．
点评：本题考查了垂线的定义．要注意领会由垂直得直角这一要点．
练习册系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
（2013•玉田县一模）如图，OA⊥OB，△CDE的边CD在OB上，∠ECD=45°．将△CDE绕点C逆时针旋转75°，点E的对应点N恰好落在OA上，则
如图，OA=OB，OC=OD，∠O=50°，∠D=30°，则∠AEC等于（ ）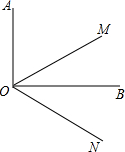
如图，OA⊥OB，OB平分∠MON，若∠AON=120°，求∠AOM的度数．
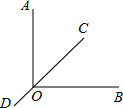如图，OA⊥OB，∠COD为平角，若OC平分∠AOB，则∠BOD=