题目内容
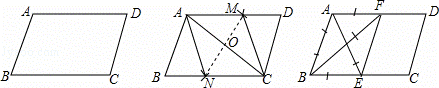
如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:
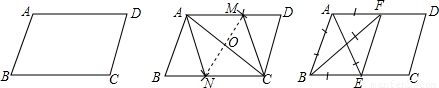
甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断
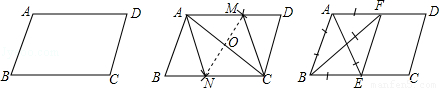
A.甲正确,乙错误 B.乙正确,甲错误 C.甲、乙均正确 D.甲、乙均错误
【答案】
C
【解析】
试题分析:甲的作法正确:
∵四边形ABCD是平行四边形,∴AD∥BC。∴∠DAC=∠ACN。
∵MN是AC的垂直平分线,∴AO=CO。
在△AOM和△CON中,∵∠MAO=∠NCO,AO=CO,∠AOM=∠CON,
∴△AOM≌△CON(ASA),∴MO=NO。∴四边形ANCM是平行四边形。
∵AC⊥MN,∴四边形ANCM是菱形。
乙的作法正确:如图,
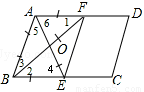
∵AD∥BC,∴∠1=∠2,∠6=∠4。
∵BF平分∠ABC,AE平分∠BAD,∴∠2=∠3,∠5=∠6。
∴∠1=∠3,∠5=∠4。∴AB=AF,AB=BE。∴AF=BE。
∵AF∥BE,且AF=BE,∴四边形ABEF是平行四边形。
∵AB=AF,∴平行四边形ABEF是菱形。
故选C。

练习册系列答案
相关题目
如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:
甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断( )
|
| A. | 甲正确,乙错误 | B. | 乙正确,甲错误 | C. | 甲、乙均正确 | D. | 甲、乙均错误 |