题目内容
四边形ABCD中,AB=CD,M、N分别为AD、BC的中点,延长BA交直线NM于E,延长CD交直线NM于F.求证:∠BEN=∠CFN.分析:取AC中点G,连接NG,MG,根据三角形中位线定理可得到NG∥AE,MG∥CF,NG=
AB,MG=
CD,由平行线的性质可得∠BEN=∠FNG,∠CFN=∠NMG,从而可推出△GMN为等腰三角形,从而不难证得结论.
| 1 |
| 2 |
| 1 |
| 2 |
解答: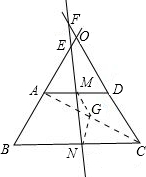 证明:取AC中点G,连接NG,MG,
证明:取AC中点G,连接NG,MG,
∵点M,G,N分别是边AD,AC,BC的中点,
∴MG是△ADC的中位线,
∴NG∥AB,MG∥CF,NG=
AB,MG=
CD,
∴∠BEN=∠FNG,∠CFN=∠NMG,
∵NG=
AB,MG=
CD,AB=CD,
∴NG=MG,
∴∠MNG=∠GMN,
∵∠MNG=∠BEN,
∠GMN=∠CFN,
∴∠BEN=∠CFN.
 证明:取AC中点G,连接NG,MG,
证明:取AC中点G,连接NG,MG,∵点M,G,N分别是边AD,AC,BC的中点,
∴MG是△ADC的中位线,
∴NG∥AB,MG∥CF,NG=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BEN=∠FNG,∠CFN=∠NMG,
∵NG=
| 1 |
| 2 |
| 1 |
| 2 |
∴NG=MG,
∴∠MNG=∠GMN,
∵∠MNG=∠BEN,
∠GMN=∠CFN,
∴∠BEN=∠CFN.
点评:此题主要考查三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 23、如图,四边形ABCD中,对角线AC、BD相交于点E.已知:DA=DC,E为AC中点.
23、如图,四边形ABCD中,对角线AC、BD相交于点E.已知:DA=DC,E为AC中点.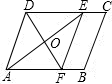 如图所示,在平行四边形ABCD中,AE是∠DAB的平分线,EF∥AD交AB于点F,若AB=9,CE=4,AE=8,则DF等于( )
如图所示,在平行四边形ABCD中,AE是∠DAB的平分线,EF∥AD交AB于点F,若AB=9,CE=4,AE=8,则DF等于( ) 17、如图,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AB、CD于E、F.请写出图中三对全等的三角形:
17、如图,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AB、CD于E、F.请写出图中三对全等的三角形: 7、如图,在四边形ABCD中,AD=CB,∠ACB=∠CAD.求证:AB=CD.
7、如图,在四边形ABCD中,AD=CB,∠ACB=∠CAD.求证:AB=CD.