题目内容
如图,已知点A(0,2),直线l:y=-x-2与x轴交于D点,与y轴交于E点,B是直线l上的一个动点,以AB为直径的圆记作⊙M.(1)判断点D是否在⊙M上,并说明理由;
(2)当⊙M与x轴相切时,求B点的坐标;
(3)若△ABE为等腰三角形,求出所有符合条件的圆心M的坐标.

【答案】分析:(1)点D在圆M上,理由为:连接AB,AD,DM,如图1所示,对于直线l,求出D与E坐标,确定出OD=OE=2,由OA=2,利用勾股定理得到AD=DE,根据三角形AOD与三角形DOE都为等腰直角三角形,可得出AD垂直于DE,在直角三角形ABD中,由斜边上的中线等于斜边的一半得到DM为直径AB的一半,即D到圆心距离等于半径,可得出D在圆M上;
(2)连接MD,AD,由∠ADB为直角,利用90度圆周角所对的弦为直径得到D在圆M上,由圆M与x轴相切,得到D为切点,进而得到BA垂直于y轴,即可确定出此时B的坐标;
(3)由B在直线y=-x-2上,设B(a,-a-2),分三种情况考虑:①A为顶点时,AB=AE,由AE长求出AB的长,确定出B的坐标,由A与B的坐标,利用线段中点坐标公式求出M坐标即可;②B为顶点时,BA=BE,此时B与D重合,求出B的坐标,利用线段中点坐标公式即可求出此时M的坐标;③E为顶点时,AE=BE,由A、B、E坐标,利用两点间的距离公式列出关于a的方程,求出方程的解得到a的值,确定出B坐标,利用线段中点坐标公式即可确定出M的坐标.
解答:
解:(1)点D在圆M上,理由为:连接AB,AD,DM,如图1所示,
对于直线l:y=-x-2,令x=0,求出y=-2;令y=0,求出x=-2,
∴D(-2,0),E(0,-2),又A(0,2),
∴OD=OE=OA=2,
根据勾股定理得:AD=ED=2 ,AE=AO+OE=4,
,AE=AO+OE=4,
∵AD2+DE2=AE2,△AOD与△DOE都为等腰直角三角形,
∴∠ADE=∠ADO+∠EDO=90°,
∴在Rt△ABD中,DM= AB,
AB,
则D在圆M上;
(2)连接MD,AD,由直线y=-x-2,可得OD=OE=2,又OA=2,
∴△ADE为等腰直角三角形,
∴∠ADB=90°,
∵AB为圆O的直径,
∴点D在圆M上,
∵圆M与x轴相切,
∴D为切点,
∴MD⊥x轴,即∠MDA+∠ADO=90°,
∵∠ADO=45°,
∴∠MDA=45°,
∵MA=MD,
∴∠MAD=∠MDA=45°,
∴∠DAE=45°,
∴∠MAD+∠DAO=90°,
∴BA⊥y轴,
∴AB=2OD=4,
则B(-4,2);
(3)设B坐标为(a,-a-2),
分三种情况考虑:
①当A为顶点时,AB=AE,B坐标为(-4,2),此时M坐标为(-2,2);
②当B为顶点时,BA=BE,B与D重合,B坐标为(-2,0),此时M坐标为(-1,1);
③当E为顶点时,BE=AE,可得BE2=AE2,即a2+(-a-2+2)2=42,解得:a1=-2 ,a2=2
,a2=2 ,
,
∴B坐标为(-2 ,2
,2 -2)或B(2
-2)或B(2 ,-2
,-2 -2),此时M(-
-2),此时M(- ,
, )或M(
)或M( ,-
,- ).
).
点评:此题属于一次函数综合题,涉及的知识有:坐标与图形性质,等腰直角三角形的判定与性质,切线的性质,圆周角定理,两点间的距离公式,线段中点坐标公式,勾股定理及逆定理,一次函数与坐标轴的交点,利用了分类讨论的思想,分类讨论时要注意不重不漏,考虑问题要全面.
(2)连接MD,AD,由∠ADB为直角,利用90度圆周角所对的弦为直径得到D在圆M上,由圆M与x轴相切,得到D为切点,进而得到BA垂直于y轴,即可确定出此时B的坐标;
(3)由B在直线y=-x-2上,设B(a,-a-2),分三种情况考虑:①A为顶点时,AB=AE,由AE长求出AB的长,确定出B的坐标,由A与B的坐标,利用线段中点坐标公式求出M坐标即可;②B为顶点时,BA=BE,此时B与D重合,求出B的坐标,利用线段中点坐标公式即可求出此时M的坐标;③E为顶点时,AE=BE,由A、B、E坐标,利用两点间的距离公式列出关于a的方程,求出方程的解得到a的值,确定出B坐标,利用线段中点坐标公式即可确定出M的坐标.
解答:

解:(1)点D在圆M上,理由为:连接AB,AD,DM,如图1所示,
对于直线l:y=-x-2,令x=0,求出y=-2;令y=0,求出x=-2,
∴D(-2,0),E(0,-2),又A(0,2),
∴OD=OE=OA=2,
根据勾股定理得:AD=ED=2
 ,AE=AO+OE=4,
,AE=AO+OE=4,∵AD2+DE2=AE2,△AOD与△DOE都为等腰直角三角形,
∴∠ADE=∠ADO+∠EDO=90°,
∴在Rt△ABD中,DM=
 AB,
AB,则D在圆M上;
(2)连接MD,AD,由直线y=-x-2,可得OD=OE=2,又OA=2,
∴△ADE为等腰直角三角形,
∴∠ADB=90°,
∵AB为圆O的直径,
∴点D在圆M上,
∵圆M与x轴相切,
∴D为切点,
∴MD⊥x轴,即∠MDA+∠ADO=90°,
∵∠ADO=45°,
∴∠MDA=45°,
∵MA=MD,
∴∠MAD=∠MDA=45°,
∴∠DAE=45°,
∴∠MAD+∠DAO=90°,
∴BA⊥y轴,
∴AB=2OD=4,
则B(-4,2);
(3)设B坐标为(a,-a-2),
分三种情况考虑:
①当A为顶点时,AB=AE,B坐标为(-4,2),此时M坐标为(-2,2);
②当B为顶点时,BA=BE,B与D重合,B坐标为(-2,0),此时M坐标为(-1,1);
③当E为顶点时,BE=AE,可得BE2=AE2,即a2+(-a-2+2)2=42,解得:a1=-2
 ,a2=2
,a2=2 ,
,∴B坐标为(-2
 ,2
,2 -2)或B(2
-2)或B(2 ,-2
,-2 -2),此时M(-
-2),此时M(- ,
, )或M(
)或M( ,-
,- ).
).点评:此题属于一次函数综合题,涉及的知识有:坐标与图形性质,等腰直角三角形的判定与性质,切线的性质,圆周角定理,两点间的距离公式,线段中点坐标公式,勾股定理及逆定理,一次函数与坐标轴的交点,利用了分类讨论的思想,分类讨论时要注意不重不漏,考虑问题要全面.

练习册系列答案
相关题目
 如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )
如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )A、
| ||||
B、
| ||||
C、2
| ||||
D、4
|
 16、如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C、下列结论错误的是( )
16、如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C、下列结论错误的是( )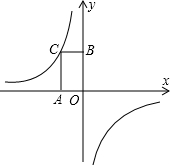 如图,已知点C为反比例函数y=-
如图,已知点C为反比例函数y=- 如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设
如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设 如图,已知点C为AB上一点,AC=12cm,CB=
如图,已知点C为AB上一点,AC=12cm,CB=