题目内容
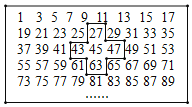
【题目】如图，将连续的奇数1，3，5，7……排成如下的数表，用十字形框框出5个数．
探究规律一：设十字框中间的奇数为x，则框中五个奇数的和用含x的整式表示为 ，这说明被十字框框中的五个奇数的和一定是正整数n（n＞1）的倍数，这个正整数n是 ；
探究规律二：落在十字框中间且位于第二列的一组奇数是21，39，57，75，…，则这一组数可以用整式表示为18m+3（m为序数），同样，落在十字框中间且位于第三列的一组奇数可以表示为 ；（用含m的式子表示）
运用规律：
（1）已知被十字框框中的五个奇数的和为2025，则十字框中间的奇数是 ，这个奇数落在从左往右第 列；
（2）被十字框框中的五个奇数的和可能是2020吗？若能，请求出这五个数：若不能，请说明理由．
【答案】探究规律一：5x、5．探究规律二：（18m+5）；（1）405、五；（2）这五个数为404、402、406、396、422．
【解析】
探究规律一：根据表中数据规律即可列出代数式进而求解；
探究规律二：根据第二列的一组奇数的规律即可写出第三列的一组奇数的规律；
（1）根据探究规律一和探究规律二所得代数式即可求解；
（2）根据探究规律一所得代数式列方程即可求解．
解：探究规律一：根据题意，得，
设十字框中间的奇数为x，则框中其它五个奇数为：
x﹣2，x+2，x﹣18，x+18．
∴x+x﹣2+x+2+x﹣18+x+18＝5x，
五个奇数的和一定是正整数n（n＞1）的倍数，这个正整数n是5．
故答案为：5x、5．
探究规律二：
因为第二列的一组奇数是21，39，57，75，…
21＝1×18+3
39＝2×18+3
57＝3×18+3
75＝4×18+3
∴这一组数可以用整式表示为18m+3（m为序数）．
∴落在十字框中间且位于第三列的一组奇数可以表示为（18m+5）．
故答案为：（18m+5）.
（1）根据题意，得
5x＝2025
解得：x＝405
∴十字框中间的奇数是405．
∵18m+9＝405，解得：m＝22，
∴405这个奇数落在从左往右第五列．
故答案为：405、五；
（2）十字框框中的五个奇数的和可以是2020．理由如下：
5x＝2020
解得：x＝404，
∴x﹣2＝402，x+2＝406，x﹣18＝396，x+18＝422．
答：这五个数为：404、402、406、396、422．
【题目】2008年6月1日起，我国实施“限塑令”，开始有偿使用环保购物袋．为了满足市场需求，某厂家生产
两种款式的布质环保购物袋，每天共生产4500个，两种购物袋的成本和售价如下表，设每天生产
种购物袋
个，每天共获利
元．
成本（元/个） | 售价（元/个） | |
| 2 | 2.3 |
| 3 | 3.5 |
（1）求出关于的函数解析式；
（2）如果该厂每天最多投入成本10000元，那么每天最多获利多少元？
