Question

如图，点D是BC的四等分点（BD＜DC），点E是AD的三等分点（DE＞AE），则AF：FC=

1：8

．

Answer 1

分析：求出DC=2BD，DE=2AE，过D作DZ∥AC交BF于Z，根据平行线得出相似，根据相似得出比例式，求出DZ=2AF，FC=4DZ，推出FC=8AF，即可得出答案．

解答：解：∵点D是BC的四等分点（BD＜DC），点E是AD的三等分点（DE＞AE），
∴DC=2BD，DE=2AE，

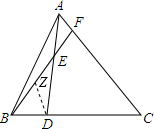
过D作DZ∥AC交BF于Z，
∴△DZE∽△AFE，△BDZ∽△BCF，
∴

DZ

AF

=

DE

AE

=

2

1

，

DZ

CF

=

BD

BC

=

1

1+3

，
∴DZ=2AF，FC=4DZ，
∴FC=8AF，
AF：FC=1：8，
故答案为：1：8．

点评：本题考查了平行线分线段成比例定理，相似三角形的性质和判定，解此题的关键是能正确作出辅助线．