题目内容
如图所示,四边形ABCD的∠BAD=∠C=90°,AB=AD,AE⊥BC于E,△BEA旋转后能与△DFA重合.(1)旋转中心是______;逆时针旋转了______度.
(2)若AE=
 ,求四边形ABCD的面积.
,求四边形ABCD的面积.
【答案】分析:(1)观察图形,△BEA旋转后能与△DFA重合,即△BEA≌△DFA,可知旋转中心,旋转角.
(2)运用割补法得出四边形ABCD的面积.等于正方形AECF的面积.
解答:解:(1)因为△BEA旋转后能与△DFA重合,所以旋转中心是A;逆时针旋转了90°;
(2)由旋转的性质可知,△BEA≌△DFA,
∴AF=AE= +
+ ,∠EAF=∠EAD+∠FAD=∠EAD+∠BAE=∠BAD=90°,
,∠EAF=∠EAD+∠FAD=∠EAD+∠BAE=∠BAD=90°,
又∵∠AEC=∠C=90°,
∴四边形AECF是正方形,
所以四边形AECF的面积为( +
+ )2=5+2
)2=5+2 ;
;
即四边形ABCD的面积为5+2 .
.
点评:本题考查旋转的性质.旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.
(2)运用割补法得出四边形ABCD的面积.等于正方形AECF的面积.
解答:解:(1)因为△BEA旋转后能与△DFA重合,所以旋转中心是A;逆时针旋转了90°;
(2)由旋转的性质可知,△BEA≌△DFA,
∴AF=AE=
 +
+ ,∠EAF=∠EAD+∠FAD=∠EAD+∠BAE=∠BAD=90°,
,∠EAF=∠EAD+∠FAD=∠EAD+∠BAE=∠BAD=90°,又∵∠AEC=∠C=90°,
∴四边形AECF是正方形,
所以四边形AECF的面积为(
 +
+ )2=5+2
)2=5+2 ;
;即四边形ABCD的面积为5+2
 .
.点评:本题考查旋转的性质.旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.

练习册系列答案
相关题目
 21、如图所示,四边形ABCD是平行四边形,E,F分别在AD,CB的延长线上,且DE=BF,连接FE分别交AB,CD于点H,G.
21、如图所示,四边形ABCD是平行四边形,E,F分别在AD,CB的延长线上,且DE=BF,连接FE分别交AB,CD于点H,G. 12、如图所示,四边形ABCD为⊙O的内接四边形,E为AB延长线的上一点,∠CBE=40°,则∠AOC等于( )
12、如图所示,四边形ABCD为⊙O的内接四边形,E为AB延长线的上一点,∠CBE=40°,则∠AOC等于( )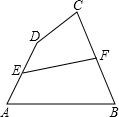 如图所示,四边形ABCD中,E、F分别为AD、BC的中点.
如图所示,四边形ABCD中,E、F分别为AD、BC的中点.
