题目内容
如图,等边三角形ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M,
则M是BE的中点,请说明理由。

:
∵等边△ABC
∴∠ABC=∠ACB=60,AB=BC
∵D是AC的中点
∴∠CBD=∠ABD=∠ABC/2=30 (三线合一)
∵CE=CD
∴∠E=∠CDE
∴∠ACB=∠E+∠CDE=2∠E
∴∠E=∠ACB/2=30
∴∠CBD=∠E
∴BD=ED
∵DM⊥BC
∴BM=DM (三线合一)

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目


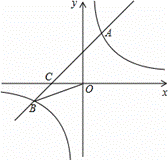
 到(1,1),而后它接着按图中箭头所示的与x轴,y轴平行的方向来回运动,且每分钟移动1个长度单位。
到(1,1),而后它接着按图中箭头所示的与x轴,y轴平行的方向来回运动,且每分钟移动1个长度单位。
 B.
B. C.
C. D.
D.
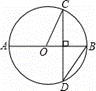
 ,则sin∠DAC的值为( )
,则sin∠DAC的值为( ) 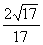 B.
B.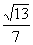 C.
C.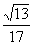 D.
D.
 a
a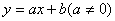 的图象与反比例函数
的图象与反比例函数 的图象交于一、三象限内的A.B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,-2),tan∠BOC=
的图象交于一、三象限内的A.B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,-2),tan∠BOC=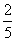 。
。