题目内容
设实数m、n满足m2n2+m2+n2+10mn+16=0,则有( )
A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|
分析:观察m2n2+m2+n2+10mn+16=0等式要求m、n的值,只需将m2n2+m2+n2+10mn+16=0转化为(mn+4)2+(m+n)2=0,再根据非负数的性质,可确定
,解得m、n即为所求值.
|
解答:解:∵m2n2+m2+n2+10mn+16=0,
∴(m2n2+8mn+16)+(m2+2mn+n2)=0,
∴(mn+4)2+(m+n)2=0,
又∵(mn+4)2≥0,(m+n)2≥0,
∴(mn+4)2=0,(m+n)2=0,
即
,
解得
或
.
故选C.
∴(m2n2+8mn+16)+(m2+2mn+n2)=0,
∴(mn+4)2+(m+n)2=0,
又∵(mn+4)2≥0,(m+n)2≥0,
∴(mn+4)2=0,(m+n)2=0,
即
|
解得
|
|
故选C.
点评:本题考查完全平方式的应用、非负数的性质.解决本题的关键是运用完全平方式将m2n2+m2+n2+10mn+16=0转化为(mn+4)2+(m+n)2=0,得到方程
,进而求出m、n的值.
|

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目

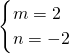
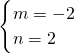 或
或