Question

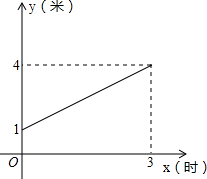（2013•甘井子区一模）底面积为3：2的A、B两个长方体蓄水池，现将A池中18立方米的水全部注入B池，用时3小时．B池中水面高度y（米）与注水时间x（时）之间的函数图象如图所示，结合图象回答下列问题：
（1）注水速度为

6

立方米/时，B水池水面上升了

3

米；
（2）从注水开始计时，多长时间两个水池的蓄水量相同；
（3）在所给坐标系中画出A池水面高度y（米）与注水时间x（时）之间的函数图象，并结合图象求出何时两水池的水面高度相差1米？

Answer 1

分析：（1）用18立方米÷时间3小时就可以求出注水速度，通过函数图象就可以求出B水池水面上升的高度；
（2）由（1）的结论求出B池原来的水量，设注水a小时时两个水池的储水量相同，求出其解即可；
（3）设甲池的底面积为3m，乙池的底面积为2m，运用容积相等建立方程就可以求出在甲池中的高度，就可以画出函数图象，分别求出两个图象的解析式就可以求出结论．

解答：解：（1）由题意，得
注水速度为：18÷3=6立方米/小时，
B池水面上升高度为：4-1=3米．

（2）由题意，得
B池原来有水：18÷3=6立方米，
设注水a小时时两个水池的储水量相同，由题意得
6+6a=18-6a，
解得：a=1，
∴从注水开始计时，1小时时两个水池的蓄水量相同；

（3）设甲池的底面积为3m，乙池的底面积为2m，A水池的水面高度为h米．由题意，得
3mh=2m×3，
m=2，
设y与x之间的函数关系式为：y_A=k₁x+b₁，由题意，得

2=b1 0=3k1+b1

，
解得：

k1=- 2 3 b1=2

，
∴y_A=-

2

3

x+2，
列表为：

x	0	3
yA=- 2 3 x+2	2	0

描点并连线为

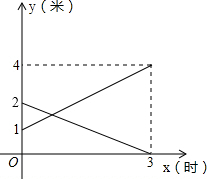
设yB=k₂x+b₂，由题意，得

1=b2 4=3k2+b2

，
解得：

k2=1 b2=1

，
∴y_B=x+1，
当y_A-y_B=1时，
-

2

3

x+2-（x+1）=1，
解得：x=0；
当y_B-y_A=1时，
x+1-（-

2

3

x+2）=1，
x=

6

5

，
∴当B池注水0小时或

6

5

小时时两水池的水面高度相差1米．
故答案为：6，3．

点评：本题是一道注水问题，考查了容积与底面积和高的数量关系的运用，待定系数法求函数的解析式的运用，描点法画函数的图象的运用，解答时弄清函数图象的意义是关键．