Question

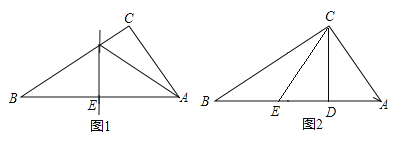
【题目】如图（1），△ABC是一个三角形的纸片，点D、E分别是△ABC边上的两点，

研究（1）：如果沿直线DE折叠，则∠BDA′与∠A的关系是 ．

研究（2）：如果折成图2的形状，猜想∠BDA′、∠CEA′和∠A的关系，并说明理由．

研究（3）：如果折成图3的形状，猜想∠BDA′、∠CEA′和∠A的关系，并说明理由．

Answer 1

【答案】（1）∠BDA′=2∠A；（2）∠BDA′+∠CEA′=2∠A；（3）∠BDA′-∠CEA′=2∠A

【解析】

试题分析：翻折问题要在图形是找着相等的量．图1中DE为折痕，有∠A=∠DA′A，再利用外角的性质可得结论∠BDA′=2∠A图2中∠A与∠DA′E是相等的，再结合四边形的内角和及互补角的性质可得结论∠BDA′+∠CEA′=2∠A图3中由于折叠∠A与∠DA′E是相等的，再两次运用三角形外角的性质可得结论．

试题解析：（1）∠BDA′=2∠A；

（2）∠BDA′+∠CEA′=2∠A，

理由：在四边形ADA′E中，∠A+∠DA′E+∠ADA′+∠A′EA=360°

∴∠A+∠DA′E=360°-∠ADA′-∠A′EA

∵∠BDA′+∠ADA′=180°，∠CEA′+∠A′EA=180°

∴∠BDA′+∠CEA′=360°-∠ADA′-∠A′EA

∴∠BDA′+∠CEA′=∠A+∠DA′E

∵△A′DE是由△ADE沿直线DE折叠而得

∴∠A=∠DA′E

∴∠BDA′+∠CEA′=2∠A；

（3）∠BDA′-∠CEA′=2∠A

理由：DA′交AC于点F，

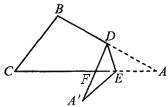
∵∠BDA′=∠A+∠DFA，∠DFA=∠A′+∠CEA′

∴∠BDA′=∠A+∠A′+∠CEA′

∴∠BDA′-∠CEA′=∠A+∠A′

∵△A′DE是由△ADE沿直线DE折叠而得

∴∠A=∠DA′E

∴∠BDA′-∠CEA′=2∠A．