Question

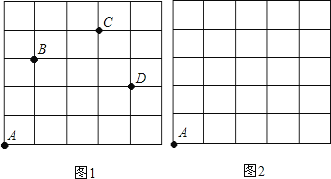
【题目】已知数轴上两点相距个单位长度，机器人从点出发去点，点在点右侧.规定向右为前进，第一次它前进个单位长度，第二次它后退个单位长度，第三次再前进个单位长度，第四次又后退个单位长度……按此规律行进，如果点在数轴上表示的数为，那么

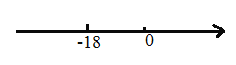
（1）求出点在数轴上表示的数.

（2）经过第七次行进后机器人到达点，第八次行进后到达点，点到点的距离相等吗？请说明理由.

（3）机器人在未到达点之前，经过次（为正整数）行进后，它在数轴上表示的数应如何用含的代数式表示？

（4）如果点在原点的右侧，那么机器人经过次行进后，它在点的什么位置？请通过计算说明.

Answer 1

【答案】（1）52；（2）点到点的距离相等；（3）或；（4）点左边个单位长度处．

【解析】

（1）根据数轴上两点之间的距离，进行计算求解；（2）根据题意分别表示出M，N所表示的数，然后根据两点间距离公式计算MA，NA的长度，从而求解；（3）分n为奇数或偶数，两种情况，根据题意列式求解；（4）将n=99代入，求值计算即可．

解：（1）由题意得，

点在数轴上表示的数为.

（2）点在数轴上表示的数为，

点在数轴上表示的数为

MA=-14-（-18）=4；NA=-18-（-22）=4

∴点到点的距离相等

（3）当为奇数时，它在数轴上表示的数为：

.

当为偶数时，它在数轴上表示的数为：

.

（4）当n=99时，

52-32=20

答：机器人经过次行进后，它在点的左边个单位长度处.