题目内容
如图所示,放在直角坐标系中的正方形ABCD的边长为4.现做如下实验:转盘被划分成三个相同的扇形,并分别标上数字1,2,3,分别转动两次转盘,转盘停止后,指针所指的数字作为直角坐标系中M点的坐标(第一次作横坐标,第二次作纵坐标),指针如果指在界线上,则重新转动转盘.(1)请你用树状图或列表的方法,求M点落在正方形ABCD面上(含内部与边界)的概率.
(2)将正方形ABCD向右至少平移多少个整数单位,使M点落在正方形ABCD面上(含内部与边界)的概率为
| 2 | 3 |
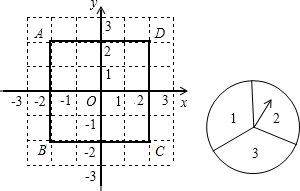
分析:(1)运用列表法得出所有的可能,即可得出M点落在正方形ABCD面上(含内部与边界)的概率;
(2)使M点落在正方形ABCD面上(含内部与边界)的概率为
,即应有六个点落在这个范围内,可以得出平移的单位个数.
(2)使M点落在正方形ABCD面上(含内部与边界)的概率为
| 2 |
| 3 |
解答:解:(1)用列表法得出:
共有9种情况,落在正方形ABCD面上(含内部与边界)有4种,
只有:(1,1),(1,2),(2,1),(2,2)符合要求;
故概率为
;
(2)∵使M点落在正方形ABCD面上(含内部与边界)的概率为
,
∴应有六个点落在这个范围内,向右至少平移1个单位,
使M点落在正方形ABCD面上(含内部与边界)的概率为
.
| 1 | 2 | 3 | |
| 1 | (1,1) | (1,2) | (1,3) |
| 2 | (2,1) | (2,2) | (2,3) |
| 3 | (3,1) | (3,2) | (3,3) |
只有:(1,1),(1,2),(2,1),(2,2)符合要求;
故概率为
| 4 |
| 9 |
(2)∵使M点落在正方形ABCD面上(含内部与边界)的概率为
| 2 |
| 3 |
∴应有六个点落在这个范围内,向右至少平移1个单位,
使M点落在正方形ABCD面上(含内部与边界)的概率为
| 2 |
| 3 |
点评:此题主要考查了列表法求概率,以及坐标与图形的性质和正方形的性质,题目综合性较强.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 ,则点C的坐标为 。
,则点C的坐标为 。
 ,0),如图所示:抛物线
,0),如图所示:抛物线 经过点B。
经过点B。
 ,则点C的坐标为
。
,则点C的坐标为
。