题目内容
如图，已知在正方形ABCD中，AB=
，E是DC的中点，则点B到直线AE的距离是________．
2
分析：过B作BF⊥AE于F，连接BE，根据勾股定理可求出AE的长，再根据三角形的面积为定值即可求出BF的长．
解答：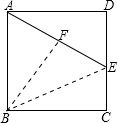
解：∵四边形ABCD是正方形，
∴∠D=90°，
∵E是DC的中点，AB=，
∴DE=
，
∴AE=
，
∵S△ABE=
AB•BC=BF•AE，
∴BF=
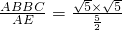=2，
∴点B到直线AE的距离是2，
故答案为：2．
点评：本题考查了正方形的性质、勾股定理的运用以及三角形的面积公式的运用，解题的关键是利用三角形ABF的面积为定值求解．
分析：过B作BF⊥AE于F，连接BE，根据勾股定理可求出AE的长，再根据三角形的面积为定值即可求出BF的长．
解答：
解：∵四边形ABCD是正方形，∴∠D=90°，
∵E是DC的中点，AB=
，∴DE=
，∴AE=
，∵S△ABE=
AB•BC=BF•AE，∴BF=
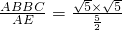=2，∴点B到直线AE的距离是2，
故答案为：2．
点评：本题考查了正方形的性质、勾股定理的运用以及三角形的面积公式的运用，解题的关键是利用三角形ABF的面积为定值求解．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
18、如图，已知在正方形ABCD中，P是BC上的一点，且AP=DP．求证：P是BC中点．
一点，连接AP．过点P作PF⊥AP，与∠DCE的平分线CF相交于点F．连接AF，与边CD相交于点G，连接PG．
如图，已知在正方形ABCD外取一点E，连接AE、BE、DE．过点A作AE的垂线交DE于点P．若AE=AP=1，PB=
（2013•仓山区模拟）如图，已知在正方形ABCD网格中，每个小方格都是边长为1的正方形，E是边DC上的一个网格的格点．
（2010•郑州模拟）如图，已知在正方形ABCD中，EF分别是AB，BC上的点，若有AE+CF=EF，请你猜想∠EDF的度数，并说明理由．