题目内容
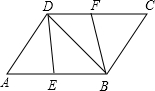
在?ABCD中,∠C的平分线交AB于点E,交DA延长线于点F,且AE=3cm,EB=5cm,则?ABCD的周长为________.
26cm
分析:首先根据题意画出图形,再根据AE=3cm,EB=5cm,求出AB=8cm,然后根据平行四边形的性质,推出AB∥CD,BC∥DF,即可推出∠F=∠BCF,由∠BCF=∠FCD,推出∠F=∠FCD,求得DF=DC=AB=8cm,再由BC∥DF,可得 ,即可求出AF的长度,既而推出AD的长度,根据平行四边形的周长求出平行四边形ABCD的周长.
,即可求出AF的长度,既而推出AD的长度,根据平行四边形的周长求出平行四边形ABCD的周长.
解答: 解:∵AE=3cm,EB=5cm,
解:∵AE=3cm,EB=5cm,
∴AB=8cm,
∵?ABCD,
∴AB∥CD,BC∥DF,AB=CD=8cm,BC=AD,
∴∠BEC=∠DCE,
∵CF是∠C的角平分线,
∴∠BCE=∠DCE,
∴∠BEC=∠BCE,
∴BC=BE=5cm,
∴AD=5cm,
∴?ABCD的周长=2BC+2AB=10+16=26cm.
故答案为26cm.
点评:本题主要考查角平分线的性质,平行线的性质,等腰三角形的判定及性质,平行四边形的性质,关键在于根据相关的性质定理推出BA和BC的长度.
分析:首先根据题意画出图形,再根据AE=3cm,EB=5cm,求出AB=8cm,然后根据平行四边形的性质,推出AB∥CD,BC∥DF,即可推出∠F=∠BCF,由∠BCF=∠FCD,推出∠F=∠FCD,求得DF=DC=AB=8cm,再由BC∥DF,可得
 ,即可求出AF的长度,既而推出AD的长度,根据平行四边形的周长求出平行四边形ABCD的周长.
,即可求出AF的长度,既而推出AD的长度,根据平行四边形的周长求出平行四边形ABCD的周长.解答:
 解:∵AE=3cm,EB=5cm,
解:∵AE=3cm,EB=5cm,∴AB=8cm,
∵?ABCD,
∴AB∥CD,BC∥DF,AB=CD=8cm,BC=AD,
∴∠BEC=∠DCE,
∵CF是∠C的角平分线,
∴∠BCE=∠DCE,
∴∠BEC=∠BCE,
∴BC=BE=5cm,
∴AD=5cm,
∴?ABCD的周长=2BC+2AB=10+16=26cm.
故答案为26cm.
点评:本题主要考查角平分线的性质,平行线的性质,等腰三角形的判定及性质,平行四边形的性质,关键在于根据相关的性质定理推出BA和BC的长度.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 如图,在?ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、BD.
如图,在?ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、BD. 如图,在?ABCD中,EF∥AB,MN∥BC,MN与EF交于点O,且O点在对角线上,图中面积相等的四边形有( )
如图,在?ABCD中,EF∥AB,MN∥BC,MN与EF交于点O,且O点在对角线上,图中面积相等的四边形有( )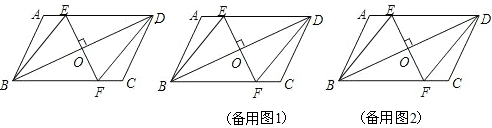
 如图,在?ABCD中,点E在边BC上,点F在BC的延长线上,且BE=CF.
如图,在?ABCD中,点E在边BC上,点F在BC的延长线上,且BE=CF.