题目内容
已知123456789101112…997998999是由连续整数1至999排列组成的一个数,在该数中从左往右数第2013位上的数字为 .
考点:
规律型:数字的变化类.
分析:
根据已知得出第2013个数字是第638个3位数的第3位,进而得出即可.
解答:
解:∵共有9个1位数,90个2位数,900个3位数
∴2013﹣9﹣90=1914,
∴![]() =638,
=638,
因此第2013个数字是第638个3位数的第3位,
第638个数为637,故第638个3位数的第3位是:7.
故答案为:7.
点评:
此题主要考查了数字变化规律,根据已知得出变化规律是解题关键.

练习册系列答案
相关题目
(本小题10分)我 校数学教研组对2011年杭州市中考数学试题的部分选择题作了错题分析统计,受污损的下表记录了n位同学的错题分布情况:
校数学教研组对2011年杭州市中考数学试题的部分选择题作了错题分析统计,受污损的下表记录了n位同学的错题分布情况:
已知这n人中,平均每题有12人答错,同时第6题答错的人数恰好是第5题答错人数的2倍,且第2题有80%的同学答对。解答下面的问题:
【小题1】(1)总共统计了多少人?
【小题2】(2) 第5,6两题各有多少人答错?
第5,6两题各有多少人答错?
【小题3】(3)将统计图 补充完整。
补充完整。
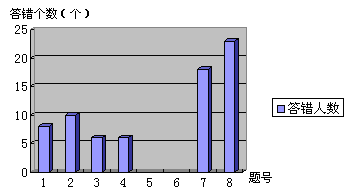
 校数学教研组对2011年杭州市中考数学试题的部分选择题作了错题分析统计,受污损的下表记录了n位同学的错题分布情况:
校数学教研组对2011年杭州市中考数学试题的部分选择题作了错题分析统计,受污损的下表记录了n位同学的错题分布情况:| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答错人数 | 9 | 10 | 6 | 6 | | | 18 | 23 |
【小题1】(1)总共统计了多少人?
【小题2】(2)
 第5,6两题各有多少人答错?
第5,6两题各有多少人答错?【小题3】(3)将统计图
 补充完整。
补充完整。
(本小题10分)我 校数学教研组对2011年杭州市中考数学试题的部分选择题作了错题分析统计,受污损的下表记录了n位同学的错题分布情况:
校数学教研组对2011年杭州市中考数学试题的部分选择题作了错题分析统计,受污损的下表记录了n位同学的错题分布情况:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答错人数 | 9 | 10 | 6 | 6 | | | 18 | 23 |
【小题1】(1)总共统计了多少人?
【小题2】(2)
 第5,6两题各有多少人答错?
第5,6两题各有多少人答错?【小题3】(3)将统计图
 补充完整。
补充完整。
我校数学教研组对2011年杭州市中考数学试题的部分选择题作了错题分析统计,受污损的下表记录了n位同学的错题分布情况:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答错人数 | 9 | 10 | 6 | 6 | | | 18 | 23 |

(1)总共统计了多少人?
(2)第5,6两题各有多少人答错?
(3)将统计图补充完整。
已知甲、乙两个班级各有50名学生.为了了解甲、乙两个班级学生解答选择题的能力状况,黄老师对某次考试中8道选择题的答题情况进行统计分析,得到统计表如下:
请根据以上信息解答下列问题:
(1)甲班学生答对的题数的众数是 ;
(2)若答对的题数大于或等于7道的为优秀,则乙班该次考试中选择题答题的优秀率= (优秀率= ×100%).
×100%).
(3)从甲、乙两班答题全对的学生中,随机抽取2人作选择题解题方法交流,则抽到的2人在同一个班级的概率等于 .
| 人数 班级 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 甲班 | 1 | 1 | 3 | 4 | 11 | 16 | 12 | 2 | |
| 乙班 | 1 | 2 | 5 | 12 | 15 | 13 | 2 |
(1)甲班学生答对的题数的众数是 ;
(2)若答对的题数大于或等于7道的为优秀,则乙班该次考试中选择题答题的优秀率= (优秀率=
 ×100%).
×100%).(3)从甲、乙两班答题全对的学生中,随机抽取2人作选择题解题方法交流,则抽到的2人在同一个班级的概率等于 .
已知甲、乙两个班级各有50名学生.为了了解甲、乙两个班级学生解答选择题的能力状况,黄老师对某次考试中8道选择题的答题情况进行统计分析,得到统计表如下:
请根据以上信息解答下列问题:
(1)甲班学生答对的题数的众数是______;
(2)若答对的题数大于或等于7道的为优秀,则乙班该次考试中选择题答题的优秀率=______(优秀率= ×100%).
×100%).
(3)从甲、乙两班答题全对的学生中,随机抽取2人作选择题解题方法交流,则抽到的2人在同一个班级的概率等于______.
 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 甲班 | 1 | 1 | 3 | 4 | 11 | 16 | 12 | 2 | |
| 乙班 | 1 | 2 | 5 | 12 | 15 | 13 | 2 |
(1)甲班学生答对的题数的众数是______;
(2)若答对的题数大于或等于7道的为优秀,则乙班该次考试中选择题答题的优秀率=______(优秀率=
 ×100%).
×100%).(3)从甲、乙两班答题全对的学生中,随机抽取2人作选择题解题方法交流,则抽到的2人在同一个班级的概率等于______.