题目内容
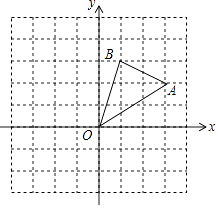
【题目】如图,已知第一象限内的点A在反比例函数y= ![]() 的图象上,第二象限内的点B在反比例函数y=
的图象上,第二象限内的点B在反比例函数y= ![]() 的图象上,且OA⊥OB,cosA=
的图象上,且OA⊥OB,cosA= ![]() ,则k的值为( )
,则k的值为( )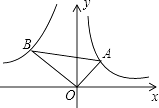
A.﹣3
B.﹣4
C.﹣ ![]()
D.﹣2 ![]()
【答案】B
【解析】解:过A作AE⊥x轴,过B作BF⊥x轴,
∵OA⊥OB,
∴∠AOB=90°,
∴∠BOF+∠EOA=90°,
∵∠BOF+∠FBO=90°,
∴∠EOA=∠FBO,
∵∠BFO=∠OEA=90°,
∴△BFO∽△OEA,
在Rt△AOB中,cos∠BAO= ![]() =
= ![]() ,
,
设AB= ![]() ,则OA=1,根据勾股定理得:BO=
,则OA=1,根据勾股定理得:BO= ![]() ,
,
∴OB:OA= ![]() :1,
:1,
∴S△BFO:S△OEA=2:1,
∵A在反比例函数y= ![]() 上,
上,
∴S△OEA=1,
∴S△BFO=2,
则k=﹣4.
故选:B.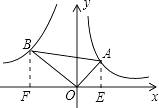
过A作AE⊥x轴,过B作BF⊥x轴,由OA与OB垂直,再利用邻补角定义得到一对角互余,再由直角三角形BOF中的两锐角互余,利用同角的余角相等得到一对角相等,又一对直角相等,利用两对对应角相等的三角形相似得到三角形BOF与三角形OEA相似,在直角三角形AOB中,由锐角三角函数定义,根据cos∠BAO的值,设出AB与OA,利用勾股定理表示出OB,求出OB与OA的比值,即为相似比,根据面积之比等于相似比的平方,求出两三角形面积之比,由A在反比例函数y= ![]() 上,利用反比例函数比例系数的几何意义求出三角形AOE的面积,进而确定出BOF的面积,再利用k的集合意义即可求出k的值.
上,利用反比例函数比例系数的几何意义求出三角形AOE的面积,进而确定出BOF的面积,再利用k的集合意义即可求出k的值.

练习册系列答案
相关题目