题目内容
如图:在菱形ABCD中,E、F为BC上两点,且BE=CF,AF=DE.求证:(1)△ABF≌△DCE;
(2)四边形ABCD是正方形.

【答案】分析:(1)先得出BF=CE,然后根据三角形的全等的判定定理结合题意所给的条件可得出结论.
(2)根据平行线的性质得出∠B+∠C=180°,结合(1)的结论可得出答案.
解答:证明:(1)∵BE=CF,
∴BF=CE,
又∵AF=DE,AB=DC,
∴△ABF≌△DCE.
(2)由△ABF≌△DCE得∠B=∠C,
由AB∥CD得∠B+∠C=180°,
得∠B=∠C=90°,
四边形ABCD是正方形.
点评:本题考查了菱形的性质及全等三角形的判定及正方形的判定,难度一般,解答本题的关键是利用已知的结论依次证明.
(2)根据平行线的性质得出∠B+∠C=180°,结合(1)的结论可得出答案.
解答:证明:(1)∵BE=CF,
∴BF=CE,
又∵AF=DE,AB=DC,
∴△ABF≌△DCE.
(2)由△ABF≌△DCE得∠B=∠C,
由AB∥CD得∠B+∠C=180°,
得∠B=∠C=90°,
四边形ABCD是正方形.
点评:本题考查了菱形的性质及全等三角形的判定及正方形的判定,难度一般,解答本题的关键是利用已知的结论依次证明.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
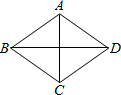 如图:在菱形ABCD中,AC=6,BD=8,则菱形的边长为( )
如图:在菱形ABCD中,AC=6,BD=8,则菱形的边长为( )| A、5 | B、10 | C、6 | D、8 |
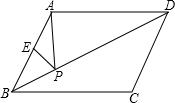
 ME交射线CD于点N,连接MD、AN.
ME交射线CD于点N,连接MD、AN. (2013•攀枝花)如图,在菱形ABCD中,DE⊥AB于点E,cosA=
(2013•攀枝花)如图,在菱形ABCD中,DE⊥AB于点E,cosA= 如图,在菱形ABCD中,AE⊥BC,垂足为F,EC=1,∠B=30°,求菱形ABCD的周长.
如图,在菱形ABCD中,AE⊥BC,垂足为F,EC=1,∠B=30°,求菱形ABCD的周长.