题目内容
直角坐标平面内，点O（0，0）、点A（3，3）、点B（3，-2），则△ABC的面积是________．
分析：根据点A、B的坐标推知AB⊥x轴．设垂足为C．由点A、B的坐标易求AB=5，OC=3．所以根据三角形的面积公式来解答问题即可．
解答：
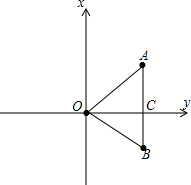解：如图，∵点A（3，3）、点B（3，-2），∴AB⊥x轴，OC=3，AB=5，
∴△ABC的面积是：
AB•OC=×5×3=．故答案是：
．点评：本题考查了三角形的面积、坐标与图形性质．根据“点A、B的坐标推知OC是△ABC的一条高线”是解题的关键．
练习册系列答案
相关题目
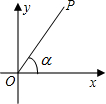如图，在直角坐标平面内，点P与原点O的距离OP=3，线段OP与x轴正半轴的夹角为α，且