Question

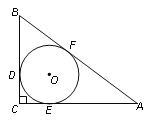
【题目】如图，在Rt△ABC中，∠ACB＝90°，⊙O是△ABC的内切圆，三个切点分别为D、E、F．若BF＝2，AF＝3，则△ABC的面积是（　　）

A. 6 B. 7 C. 12 D. 7

Answer 1

【答案】A

【解析】

利用切线的性质以及正方形的判定方法得出四边形OECD是正方形，进而利用勾股定理得出答案．

连接DO，EO，

∵⊙O是△ABC的内切圆，切点分别为D，E，F，

∴OE⊥AC，OD⊥BC，CD=CE，BD=BF=2，AF=AE=3

又∵∠C=90°，

∴四边形OECD是矩形，

又∵EO=DO，

∴矩形OECD是正方形，

设EO=x，

则EC=CD=x，

在Rt△ABC中

BC2+AC2=AB2

故（x+2）2+（x+3）2=52，

解得：x=1，x=-6(舍去)

∴BC=3，AC=4，

∴S△ABC=×3×4=6，

故选A．