题目内容
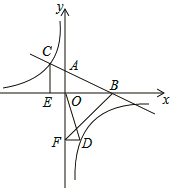
【题目】如图,四边形ABCD为正方形,点E在边 AB上,点F在AB的延长线上,点G在边AD上,且EF= ![]() AB,DG=
AB,DG= ![]() AE,连接DE、FG相交于点H.
AE,连接DE、FG相交于点H.
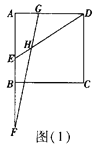
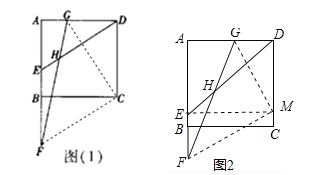
(1)若![]() ,如图(1),求∠EHF的度数(提示:连接CG,CF);
,如图(1),求∠EHF的度数(提示:连接CG,CF);
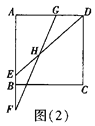
(2)若![]() ,如图(2),求tan∠EHF的值.
,如图(2),求tan∠EHF的值.
【答案】(1)45°;(2)![]()
【解析】分析:(1)连接FC和CG(如图1),先证明△AED≌△DGC,同理△FBC≌△EAD,再证明△GFC是等腰直角三角形即可.
(2)如图2,过点F作FM∥ED交CD于M,连接GM,先证明△DGM∽△AED,得∠ADE=∠DMG, ![]() =
=![]() =
=![]() ,再证明△FMG是直角三角形即可.
,再证明△FMG是直角三角形即可.
详解:(1)连接FC和CG(如图1).
∵四边形ABCD为正方形,AE=BF=GD,∴AB=BC=DC=AD,∠A=∠ABC=∠FBC=∠CDG=90°.在△EAD和△GDC中, 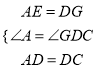 ,∴△AED≌△DGC(SAS),同理△FBC≌△EAD,∴CF=GC,∠AED=∠BFC,∠BCF=∠DCG,∴ED∥FC,∴∠EHF=∠GFC.
,∴△AED≌△DGC(SAS),同理△FBC≌△EAD,∴CF=GC,∠AED=∠BFC,∠BCF=∠DCG,∴ED∥FC,∴∠EHF=∠GFC.
又∵∠BCD=90°=∠BCG+∠GCD=∠BCG+∠BCF=∠GCF,∴△GCF是等腰直角三角形,∴∠GFC=∠FGC=45°,∴∠EHF=45°;
(2)如图2,过点F作FM∥ED交CD于M,连接GM.
∵正方形ABCD中,AB∥CD,∴四边形EFMD为平行四边形,∴EF=DM,DE=FM,∴∠3=∠4,∠EHF=∠HFM=α.
∵EF=![]() CD,GD=
CD,GD=![]() AE,∴
AE,∴![]() .
.
∵∠A=∠GDM=90°,∴△DGM∽△AED,∴∠ADE=∠DMG, ![]() =
=![]() =
=![]()
∵∠DMG+∠MGD=90°,∴∠ADE+∠DGM=90°,∴GM⊥DE.
∵ED∥FM,∴GM⊥FM,∠EHF=∠GFM,∴tan∠GFM=![]() =
=![]() =
=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目