题目内容
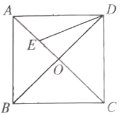
【题目】如图,正方形ABCD的对角线AC,BD交于点O,DE平分![]() 交OA于点E,若
交OA于点E,若![]() ,则线段OE的长为________.
,则线段OE的长为________.
【答案】2-![]()
【解析】
由正方形的性质可得AB=CD,∠COD=90°,OC=OD,∠ADB=∠ACD=∠CDO=45°,又因DE平分∠ODA,所以∠BDE=∠ADE=22.5°;在△ADE中,根据三角形的内角和定理可得∠CED=67.5°,所以∠CED=∠CDE=67.5°;根据等腰三角形的性质可得CD=CE=2;在等腰Rt△COD中,根据勾股定理求得OC=![]() ,由此即可求得OE的长.
,由此即可求得OE的长.
∵四边形ABCD为正方形,
∴AB=CD,∠COD=90°,OC=OD,∠ADB=∠ACD=∠CDO=45°,
∵DE平分![]() ,
,
∴∠BDE=∠ADE=22.5°,
∴∠CDE=∠BDE+∠CDO =67.5°;
在△ADE中,根据三角形的内角和定理可得∠CED=67.5°,
∴∠CED=∠CDE=67.5°,
∴CD=CE=2,
在等腰Rt△COD中,根据勾股定理求得OC=![]() ,
,
∴OE=CE-OC=2-![]() .
.
故答案为:2-![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目