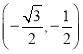Question

【题目】（定义）连结三角形一个顶点及这个顶点所对边上的任意一点，若构成的线段能将三角形分割成两个等腰三角形，则称这条线段是这个三角形的完美分割线．

（尝试）

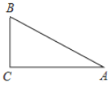
（1）如图，在 Rt△ABC 中，∠C＝90°，∠A＝30°，请用直尺和圆规画出△ABC 的完美分割线．

（2）若一个直角三角形有两条完美分割线，请求出这个直角三角形最小内角的度数．

（探究）

（3）一个等腰三角形的腰长为 8，其中一条完美分割线分得的两个三角形中有一个三角形与原三角形相似，求对应完美分割线的长度．

Answer 1

【答案】（1）见解析；（2）22.5度；（3）完美分割线的长度为或

【解析】

（1）作AB边的垂直平分线交AB于P，连接CP，则线段CP即为△ABC 的完美分割线；

（2）根据完美分割线的定义可知，直角三角形有两条完美分割线时，其中一条是斜边上的中线，另一条会构成等腰直角三角形，据此求解即可；

（3）分三种情况讨论：①当原三角形为锐角三角形时，②当原三角形为直角三角形时，③当原三角形为钝角三角形时，分别作出图形，利用相似三角形的性质计算即可．

解：（1）如图所示，线段CP即为△ABC 的完美分割线；

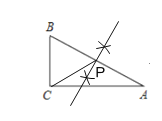
（2）∵直角三角形有两条完美分割线，

∴其中一条是斜边上的中线，另一条会构成等腰直角三角形，

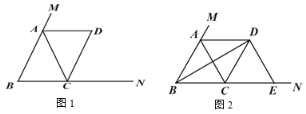
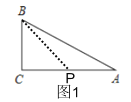
如图1，∠C＝90°，BC＝CP，PB＝PA，

∴∠CBP＝∠CPB＝45°，

∴∠A＝∠PBA＝22.5°，

∴∠ABC＝90°－22.5°＝67.5°，

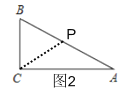
如图2，P为AB中点，则PB＝PC＝PA，

即CP也是△ABC的完美分割线，

故这个直角三角形最小内角的度数为22.5°；

（3）①当原三角形为锐角三角形时，如图所示，BP为完美分割线，

设BP＝x，

∵AB＝AC＝8，△ABC∽△BCP，

∴，即，

解得：或（舍去），

即完美分割线BP的长度为；

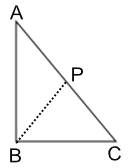
②当原三角形为直角三角形时，由题意可知该三角形为等腰直角三角形，如图所示，BP为完美分割线，

∵AB＝BC＝8，

∴AC＝，

∴BP＝，

即完美分割线BP的长度为；

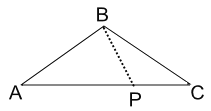
③当原三角形为钝角三角形时，如图所示，BP为完美分割线，

设BP＝x，

∵BA＝BC＝8，△BPC∽△CBA，

∴，即，

得：或（舍去），

即完美分割线BP的长度为；

综上：对应完美分割线的长度为或．