题目内容
将一条宽度为1的长方形纸条，按图所示的方式向上折叠，当∠AOB=α时，阴影部分的面积为
- A.AC
- B.
- C.
- D.
C
分析：易证得Rt△ANC≌Rt△AMD，得到AN=AM，则四边形AMON为菱形，在Rt△AMD中，∠AMD=2α，AD=1，利用正弦的定义表示出AM=
，然后根据三角形的面积公式计算即可．
解答：
解：如图，AC=AD=1，
∴∠CAN=∠MAD=90°-∠NAM，
∴Rt△ANC≌Rt△AMD，
∴AN=AM，
∴四边形AMON为菱形，
在Rt△AMD中，∠AMD=2α，AD=1，
∴sin∠AMD=
，
∴AM=，
∴S阴影部分=••1=．
故选C．
点评：本题考查了折叠的性质：折叠前后的两个图形全等，即对应角相等，对应线段相等．也考查了三角函数的定义．
分析：易证得Rt△ANC≌Rt△AMD，得到AN=AM，则四边形AMON为菱形，在Rt△AMD中，∠AMD=2α，AD=1，利用正弦的定义表示出AM=
，然后根据三角形的面积公式计算即可．解答：
解：如图，AC=AD=1，∴∠CAN=∠MAD=90°-∠NAM，
∴Rt△ANC≌Rt△AMD，
∴AN=AM，
∴四边形AMON为菱形，
在Rt△AMD中，∠AMD=2α，AD=1，
∴sin∠AMD=
，∴AM=
，∴S阴影部分=
••1=．故选C．
点评：本题考查了折叠的性质：折叠前后的两个图形全等，即对应角相等，对应线段相等．也考查了三角函数的定义．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图是某区“平改坡”工程中一种坡屋顶的设计图．已知原平屋顶的宽度AB为8米，两条相等的斜面钢条AC、BC夹角为110°，过点C作CD⊥AB于D．
是雨天，8天是阴天，其余是晴天．最多．
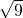的值为
在一幅长60cm，宽40cm的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂图，如图所示，如果要使整个挂图的面积是ycm2，设金色纸边的宽度为xcm2，那么y关于x的函数是