题目内容
在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论: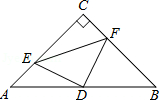
①△DFE是等腰直角三角形;
②四边形CEDF不可能为正方形;
③四边形CEDF的面积随点E位置的改变而发生变化;
④点C到线段EF的最大距离为 .
.
其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
B
解析试题分析:①作常规辅助线连接CD,由SAS定理可证△CDF和△ADE全等,从而可证∠EDF=90°,DE=DF.所以△DFE是等腰直角三角形;
②当E为AC中点,F为BC中点时,四边形CEDF为正方形;
③由割补法可知四边形CEDF的面积保持不变;
④△DEF是等腰直角三角形, DE=EF,当DF与BC垂直,即DF最小时,FE取最小值
DE=EF,当DF与BC垂直,即DF最小时,FE取最小值 ,此时点C到线段EF的最大距离.
,此时点C到线段EF的最大距离.
①连接CD
∵△ABC是等腰直角三角形,
∴∠DCB=∠A=45°,CD=AD=DB;
∵AE=CF,
∴△ADE≌△CDF;
∴ED=DF,∠CDF=∠EDA;
∵∠ADE+∠EDC=90°,
∴∠EDC+∠CDF=∠EDF=90°,
∴△DFE是等腰直角三角形.故此选项正确;
②当E、F分别为AC、BC中点时,四边形CDFE是正方形,故此选项错误;
③如图所示,分别过点D,作DM⊥AC,DN⊥BC,于点M,N,
可以利用割补法可知四边形CEDF的面积等于正方形CMDN面积,故面积保持不变;故此选项错误;
④△DEF是等腰直角三角形, DE=EF,
DE=EF,
当EF∥AB时,
∵AE=CF,
∴E,F分别是AC,BC的中点,故EF是△ABC的中位线,
∴EF取最小值 ,
,
∵CE=CF=2,
∴此时点C到线段EF的最大距离为 ,故此选项正确;
,故此选项正确;
故正确的有2个,
故选B.
考点:全等三角形的判定与性质,正方形、等腰三角形、直角三角形性质
点评:根据图形利用割补法可知四边形CEDF的面积等于正方形CMDN面积是解题关键.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案A、
| ||
B、
| ||
C、
| ||
D、
|
| 2 |
| 6 |
| 2 |
A、
| ||
B、
| ||
| C、2 | ||
| D、以上都不对 |
 23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
 18、如图,在△ABC中,边AC的垂直平分线交BC于点D,交AC于点E、已知△ABC中与△ABD的周长分别为18cm和12cm,则线段AE的长等于
18、如图,在△ABC中,边AC的垂直平分线交BC于点D,交AC于点E、已知△ABC中与△ABD的周长分别为18cm和12cm,则线段AE的长等于