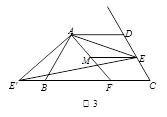
题目内容
如图Rt△ABC中,∠ACB=90°,∠B=30°,AC=1,且AC在直线l上,将△ABC绕点A顺时针旋转到①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+ ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+ ;…按此规律继续旋转,直到点P2012为止,则AP2012等于( )
;…按此规律继续旋转,直到点P2012为止,则AP2012等于( )

 ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+ ;…按此规律继续旋转,直到点P2012为止,则AP2012等于( )
;…按此规律继续旋转,直到点P2012为止,则AP2012等于( )
A.2 011+671 | B.2 012+671 |
C.2 013+671 | D.2 014+671 |
B
∵Rt△ABC中,∠ACB=90°,∠B=30°,
AC=1,∴AB=2,BC= ,∴将△ABC绕点A顺时针旋转到①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+
,∴将△ABC绕点A顺时针旋转到①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+ ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=2+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=2+ +1=3+
+1=3+ ;又∵2 012÷3=670…2,
;又∵2 012÷3=670…2,
∴AP2 012=670(3+ )+2+
)+2+ =2 012+671
=2 012+671 .
.
AC=1,∴AB=2,BC=
 ,∴将△ABC绕点A顺时针旋转到①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+
,∴将△ABC绕点A顺时针旋转到①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+ ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=2+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=2+ +1=3+
+1=3+ ;又∵2 012÷3=670…2,
;又∵2 012÷3=670…2,∴AP2 012=670(3+
 )+2+
)+2+ =2 012+671
=2 012+671 .
.
练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目


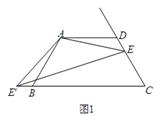
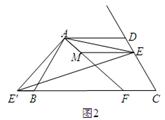
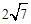 ,求ME的长.
,求ME的长.