��Ŀ����
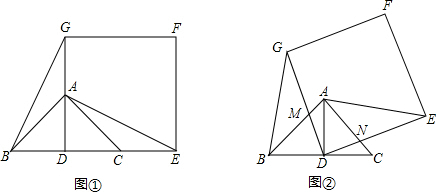
��2012•������ģ�⣩��ͼ�٣���֪��ABC�ǵ���ֱ�������Σ���BAC=90�㣬BC=2��AD��BC���ϵĸߣ���������DEFG��ʹ��A��C�ֱ���DG��DE�ϣ���DE=BC��������AE��BG��
��1���Բ����߶�BG��AE��������ϵ����ֱ��д����õ��Ľ��ۣ�
��2����������DEFG�Ƶ�D��ʱ�뷽����תһ���ǶȺ���ת�Ƕȴ���0�㣬��С��90�㣩��DG��DE�ֱ�AB��AC�ڵ�M��N����ͼ�ڣ�����1���еĽ����Ƿ���Ȼ���������������������֤�����������������˵�����ɣ�
��3���ڣ�2��������£���AE��BCʱ����AM��ֵ��
��1���Բ����߶�BG��AE��������ϵ����ֱ��д����õ��Ľ��ۣ�
��2����������DEFG�Ƶ�D��ʱ�뷽����תһ���ǶȺ���ת�Ƕȴ���0�㣬��С��90�㣩��DG��DE�ֱ�AB��AC�ڵ�M��N����ͼ�ڣ�����1���еĽ����Ƿ���Ȼ���������������������֤�����������������˵�����ɣ�
��3���ڣ�2��������£���AE��BCʱ����AM��ֵ��

��������1������BG=AE����Rt��BDG��Rt��EDA�����ݱ߽DZ߶�����Rt��BDG��Rt��EDA����BG=AE��
��2����1���еĽ�����Ȼ����������AD������ֱ���������������ε����ʿɵ�Rt��BDG��Rt��EDA�������ɵ�BG=AE��
��3������Ϊ��ABC�ǵ���ֱ�������Σ�AD��BC���ϵĸߣ����á����ߺ�һ����֤��BD=CD������֤����BDM�ա�ADN������BM=AN�����ù��ɶ������AE����ͨ��֤����ADM�ס�AEN��
�������������ε����ʵõ�����AM�ı���ʽ������֪���ݴ������AM��ֵ���ɣ�
��2����1���еĽ�����Ȼ����������AD������ֱ���������������ε����ʿɵ�Rt��BDG��Rt��EDA�������ɵ�BG=AE��
��3������Ϊ��ABC�ǵ���ֱ�������Σ�AD��BC���ϵĸߣ����á����ߺ�һ����֤��BD=CD������֤����BDM�ա�ADN������BM=AN�����ù��ɶ������AE����ͨ��֤����ADM�ס�AEN��
�������������ε����ʵõ�����AM�ı���ʽ������֪���ݴ������AM��ֵ���ɣ�
�����1������BG=AE��
֤�����ߡ�ABC�ǵ���ֱ�������Σ�AD��BC��
��BD=DA��
��������DEFG��GD=DE����GDB=��EDA��
��Rt��BDG��Rt��ADE��
��Rt��BDG��Rt��ADE��SAS����
��BG=AE��
��2����1���еĽ�����Ȼ�������������£�
��Rt��BAC�У�DΪб��BC���е㣬
��AD=BD��AD��BC��
���ADG+��GDB=90�㣬
��EFGD������
��DE=DG���ҡ�GDE=90�㣬
���ADG+��ADE=90�㣬
���BDG=��ADE��
�ڡ�BDG�͡�AED�У�
��
���BDG�ա�ADE��SAS����
��BG=AE��
��3���ߡ�ABC�ǵ���ֱ�������Σ�AD��BC���ϵĸߣ�
���5=��6=��7=45�㣬
��BD=AD����3=��2��
���BDM�ա�ADN��
��BM=AN��
��AB=BC•cos��7=2cos45��=
��
��AN=BM=AB-AM=
-AM��
��AE��BC��
���EAD=180��-��ADC=90�㣬
��AD=
BC=
��1=1��DE=BC=2��
��AE=
=
��
�ߡ�1+��2=90�㣬��2+��4=90�㣬
���1=��4��
�ߡ�8=90��-��6=45�㣬
���5=��8��
���ADM�ס�AEN��
��
=
��
��
=
��
��AM=
��
֤�����ߡ�ABC�ǵ���ֱ�������Σ�AD��BC��
��BD=DA��
��������DEFG��GD=DE����GDB=��EDA��
��Rt��BDG��Rt��ADE��
|
��Rt��BDG��Rt��ADE��SAS����
��BG=AE��
��2����1���еĽ�����Ȼ�������������£�
��Rt��BAC�У�DΪб��BC���е㣬
��AD=BD��AD��BC��
���ADG+��GDB=90�㣬
��EFGD������
��DE=DG���ҡ�GDE=90�㣬
���ADG+��ADE=90�㣬
���BDG=��ADE��
�ڡ�BDG�͡�AED�У�
|

���BDG�ա�ADE��SAS����
��BG=AE��
��3���ߡ�ABC�ǵ���ֱ�������Σ�AD��BC���ϵĸߣ�
���5=��6=��7=45�㣬
��BD=AD����3=��2��
���BDM�ա�ADN��
��BM=AN��
��AB=BC•cos��7=2cos45��=
| 2 |
��AN=BM=AB-AM=
| 2 |
��AE��BC��
���EAD=180��-��ADC=90�㣬
��AD=
| 1 |
| 2 |
| 1 |
| 2 |
��AE=
| DE2-AD2 |
| 3 |
�ߡ�1+��2=90�㣬��2+��4=90�㣬
���1=��4��
�ߡ�8=90��-��6=45�㣬
���5=��8��
���ADM�ס�AEN��
��
| AD |
| AE |
| AM |
| AN |
��
| 1 | ||
|
| AM | ||
|
��AM=
| ||||
| 2 |
���������⿼�������ε����ʡ�����ֱ�������ε����ʡ�ȫ�������ε��ж��������Լ����������ε��ж������ʣ���Ŀ���ۺ��Ժ�ǿ�������Ҫ������������ε��������ʣ�ע�����������е����������ε�Ӧ�ã��������е������ε����߹�ϵ������������߽����ٶȺ�ȷ�ʣ�

��ϰ��ϵ�д�
�����Ŀ
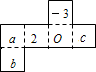 ��2012•������ģ�⣩��ͼ��һ��������ֽ�е�չ��ͼ���������۳��������������ϵ���������Ϊ�෴������ca+b=��������
��2012•������ģ�⣩��ͼ��һ��������ֽ�е�չ��ͼ���������۳��������������ϵ���������Ϊ�෴������ca+b=�������� ��2012•������ģ�⣩��ͼ��һ���������ŵ����Ų��ֵ�ʾ��ͼ�����ŵ�ͨ�������λ���ƽ��¥��AD��BE��һ��ˮƽƽ̨DE���ɣ���֪��A=37�㣬AD=5�ף�DE=1.6�ף�BE=3�ף������ŵĸ߶�BC�����ŵ�ˮƽ���AC�ij����ο����ݣ�ȡsin37��=0.60��cos37��=0.80��tan37��=0.75��
��2012•������ģ�⣩��ͼ��һ���������ŵ����Ų��ֵ�ʾ��ͼ�����ŵ�ͨ�������λ���ƽ��¥��AD��BE��һ��ˮƽƽ̨DE���ɣ���֪��A=37�㣬AD=5�ף�DE=1.6�ף�BE=3�ף������ŵĸ߶�BC�����ŵ�ˮƽ���AC�ij����ο����ݣ�ȡsin37��=0.60��cos37��=0.80��tan37��=0.75�� ��2012•������ģ�⣩��ͼ������OABC��AB��OC����B=90�㣬BC=2���ױ�OC��x���غϣ���DΪBC���е㣬��AD��OD��
��2012•������ģ�⣩��ͼ������OABC��AB��OC����B=90�㣬BC=2���ױ�OC��x���غϣ���DΪBC���е㣬��AD��OD��