题目内容
点P1（
1，
1），点P2（2，2）是一次函数＝－4 + 3 图象上的两个点，且1＜2，则1与2的大小关系是（ ）
A． 1＞2 | B．1＞2＞0 | C．1＜2 | D．1＝2 |
A
解析试题分析：根据题意，k=-4＜0，y随x的增大而减小，因为x1＜x2，所以y1＞y2．
考点：一次函数图象上点的坐标特征
练习册系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
若一次函数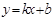
，当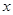
的值减小1,
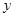的值就减小2，则当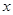的值增加2时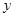，的值( )
| A．减小2 | B．增加2 | C．减小 4 | D．增加4 |
如图，函数
和
的图象相交于A(m，3),则不等式
的解集为
A． &nbs, | B． &nbs, | C． &nbs, | D． &nbs, |
若函数
是一次函数，则
应满足的条件是（ ）
A． 且 | B． 且 |
| C．且 | D．且 |
对于点A（x1，y1），B（x2，y2），定义一种运算：
．例如，A（－5，4），B（2，﹣3），
．若互不重合的四点C，D，E，F，满足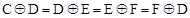
，则C，D，E，F四点【 】
| A．在同一条直线上&nbs, | B．在同一条抛物线上&nbs, |
| C．在同一反比例函数图象上&nbs, | D．是同一个正方形的四个顶点&nbs, |
如果一个正比例函数的图象经过不同象限的两点A（2，m），B（n，３），那么一定有【 】
| A．m>0，n>0&nbs, | B．m>0，n<0 &nbs, | C．m<0，n>0&nbs, | D．m<0，n<0&nbs, |
