Question

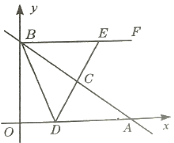
【题目】如图，在平面直角坐标系中，直线分别交轴于两点，为线段的中点，是线段上一动点（不与点重合），射线轴，延长交于点．

（1）求证：；

（2）连接，记的面积为，求关于的函数关系式；

（3）是否存在的值，使得是以为腰的等腰三角形？若存在，求出所有符合条件的的值；若不存在，请说明理由．

Answer 1

【答案】（1）详见解析；（2）；（3）存在，当或时，使得是以为腰的等腰三角形．

【解析】

（1）先判断出，，再判断出，进而判断出△BCE≌△ACD，即可得出结论；

（2）先确定出点，坐标，再表示出，即可得出结论；

（3）分两种情况：当时，利用勾股定理建立方程，即可得出结论；当时，先判断出Rt△OBD≌Rt△MED，得出，再用建立方程求解即可得出结论．

解：（1）证明：射线轴，

，，

又为线段的中点，

，

在△BCE和△ACD中，

，

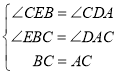∴△BCE≌△ACD（AAS），

；

（2）解：在直线中，

令，则，

令，则，

点坐标为，点坐标为，

点坐标为，

，

；

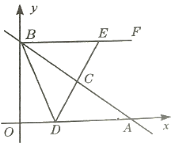
（3）当时，

在中，，

由勾股定理得：，

即

解得：；

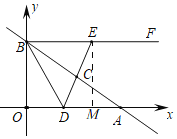
当时，

过点作轴于，

，

，

在Rt△OBD和Rt△MED中，

，

∴Rt△OBD≌Rt△MED（HL），

，

由得： 解得：，

综上所述，当或时，使得△BDE是以为腰的等腰三角形．