题目内容
将长为64的绳分成两段,各自围成两个大小不一样的正方形,这两个正方形的边长之差为2,求以这两个正方形边长为长和宽的矩形的面积.________
63
分析:设这两个正方形的边长分别为a,b,且a>b.根据这两个正方形的边长关系,列出方程组,求得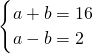 ,利用平方差公式计算,求出两个正方形边长为长和宽的矩形的面积.
,利用平方差公式计算,求出两个正方形边长为长和宽的矩形的面积.
解答:设这两个正方形的边长为分别为a,b,且a>b.
由题意得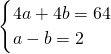 ,
,
整理得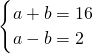
所以ab= [(a+b)2-(a-b)2]
[(a+b)2-(a-b)2]
= (162-22)
(162-22)
= (16+2)(16-2)
(16+2)(16-2)
=63,
所以以a,b为边长的矩形面积为63.
点评:运用平方差公式计算时,关键要找相同项和相反项,其结果是相同项的平方减去相反项的平方.解答本题要设出这两个正方形的边长为分别为a,b,且a>b.
分析:设这两个正方形的边长分别为a,b,且a>b.根据这两个正方形的边长关系,列出方程组,求得
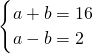 ,利用平方差公式计算,求出两个正方形边长为长和宽的矩形的面积.
,利用平方差公式计算,求出两个正方形边长为长和宽的矩形的面积.解答:设这两个正方形的边长为分别为a,b,且a>b.
由题意得
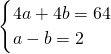 ,
,整理得
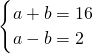
所以ab=
 [(a+b)2-(a-b)2]
[(a+b)2-(a-b)2]=
 (162-22)
(162-22)=
 (16+2)(16-2)
(16+2)(16-2)=63,
所以以a,b为边长的矩形面积为63.
点评:运用平方差公式计算时,关键要找相同项和相反项,其结果是相同项的平方减去相反项的平方.解答本题要设出这两个正方形的边长为分别为a,b,且a>b.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目