题目内容
 如图,在△ABC中,BC=AC,∠C=90°,BD是角平分线,请说明AB=BC+CD.
如图,在△ABC中,BC=AC,∠C=90°,BD是角平分线,请说明AB=BC+CD.考点:角平分线的性质,全等三角形的判定与性质
专题:证明题
分析:过点D作DM⊥AB于点M,根据ASA定理得出△DMB≌△DCB,再由全等三角形的性质即可得出结论.
解答:解: 过点D作DM⊥AB于点M,
过点D作DM⊥AB于点M,
∵BD是角平分线,
∴DC=DM.
在△DBM与△DBC中,
∵
,
∴△DMB≌△DCB(ASA).
∴BC=BM.
∵BC=AC,∠C=90°,
∴∠A=45°,
∴AM=DM=DC,
∴AB=BC+CD.
 过点D作DM⊥AB于点M,
过点D作DM⊥AB于点M,∵BD是角平分线,
∴DC=DM.
在△DBM与△DBC中,
∵
|
∴△DMB≌△DCB(ASA).
∴BC=BM.
∵BC=AC,∠C=90°,
∴∠A=45°,
∴AM=DM=DC,
∴AB=BC+CD.
点评:本题考查的是角平分线的性质,熟知角的平分线上的点到角的两边的距离相等是解答此题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
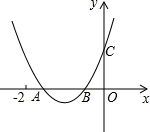 如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,且OB=OC,下列结论:①b>1且b≠2;②b2-4ac<4a2;③a>
如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,且OB=OC,下列结论:①b>1且b≠2;②b2-4ac<4a2;③a>| 1 |
| 2 |
| A、0 | B、1 | C、2 | D、3 |
 在△ABC中,O为∠CAB和∠CBA的角平分线的交点,若∠AOB=120°,则∠C的度数为( )
在△ABC中,O为∠CAB和∠CBA的角平分线的交点,若∠AOB=120°,则∠C的度数为( )| A、120° | B、60° |
| C、50° | D、30 |
 如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,此操作的依据是
如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,此操作的依据是